scipy.signal.

czt#

scipy.signal.czt(x, m=None, w=None, a=1 + 0j, *, axis=-1)[Quelle]#

Berechnet die Frequenzantwort um eine Spirale in der Z-Ebene.

Parameter:

xarray: Das zu transformierende Signal.
mint, optional: Die Anzahl der gewünschten Ausgabepunkte. Standard ist die Länge der Eingabedaten.
wcomplex, optional: Das Verhältnis zwischen den Punkten in jedem Schritt. Dies muss präzise sein, da sonst akkumulierte Fehler das Ende der Ausgabesequenz beeinträchtigen. Standardmäßig gleichmäßig verteilte Punkte um den gesamten Einheitskreis.
acomplex, optional: Der Startpunkt in der komplexen Ebene. Standard ist 1+0j.
axisint, optional: Achse, entlang derer die FFT berechnet werden soll. Wenn nicht angegeben, wird die letzte Achse verwendet.

Rückgabe:

outndarray: Ein Array mit denselben Dimensionen wie x, aber mit der Länge der transformierten Achse auf m gesetzt.

Siehe auch

CZT: Klasse, die eine aufrufbare Chirp-Z-Transformation-Funktion erstellt.
zoom_fft: Hilfsfunktion für partielle FFT-Berechnungen.

Hinweise

Die Standardwerte sind so gewählt, dass signal.czt(x) äquivalent zu fft.fft(x) ist und, wenn m > len(x), dass signal.czt(x, m) äquivalent zu fft.fft(x, m) ist.

Wenn die Transformation wiederholt werden muss, verwenden Sie CZT, um eine spezialisierte Transformationsfunktion zu erstellen, die wiederverwendet werden kann, ohne Konstanten neu zu berechnen.

Eine beispielhafte Anwendung findet sich in der Systemidentifikation, wo wiederholt kleine Ausschnitte der Z-Transformation eines Systems ausgewertet werden, um die Schätzung der wahren Lage eines Pols zu verfeinern, in dessen Nähe man einen Pol erwartet. [1]

Referenzen

[1]

Steve Alan Shilling, „A study of the chirp z-transform and its applications“, S. 20 (1970) https://krex.k-state.edu/dspace/bitstream/handle/2097/7844/LD2668R41972S43.pdf

Beispiele

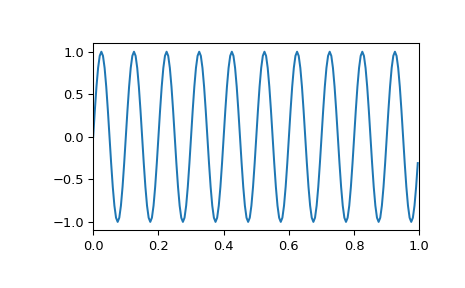
Erzeuge eine Sinuskurve

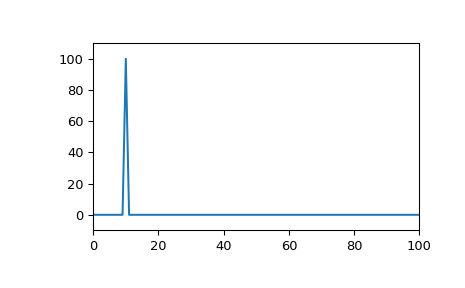
>>> import numpy as np
>>> f1, f2, fs = 8, 10, 200  # Hz
>>> t = np.linspace(0, 1, fs, endpoint=False)
>>> x = np.sin(2*np.pi*t*f2)
>>> import matplotlib.pyplot as plt
>>> plt.plot(t, x)
>>> plt.axis([0, 1, -1.1, 1.1])
>>> plt.show()

Ihre diskrete Fourier-Transformation hat die gesamte Energie in einem einzigen Frequenz-Bin

>>> from scipy.fft import rfft, rfftfreq
>>> from scipy.signal import czt, czt_points
>>> plt.plot(rfftfreq(fs, 1/fs), abs(rfft(x)))
>>> plt.margins(0, 0.1)
>>> plt.show()

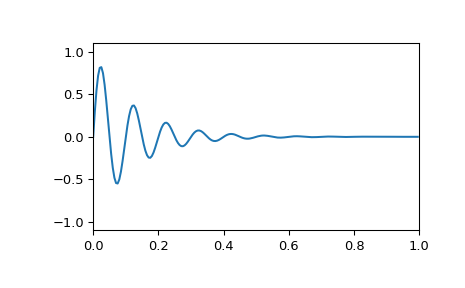
Wenn die Sinuskurve jedoch logarithmisch abfällt

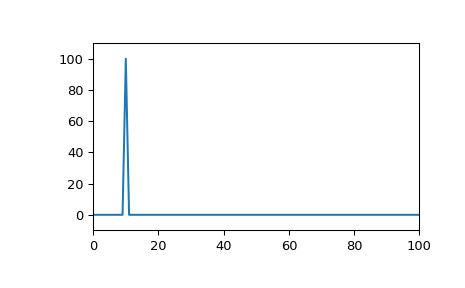
>>> x = np.exp(-t*f1) * np.sin(2*np.pi*t*f2)
>>> plt.plot(t, x)
>>> plt.axis([0, 1, -1.1, 1.1])
>>> plt.show()

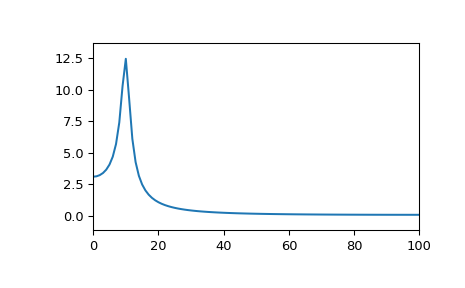
wird die DFT spektrale Leckage aufweisen

>>> plt.plot(rfftfreq(fs, 1/fs), abs(rfft(x)))
>>> plt.margins(0, 0.1)
>>> plt.show()

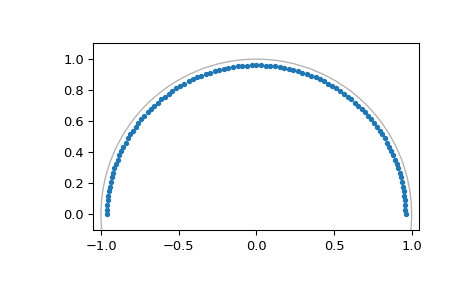
Während die DFT immer die Z-Transformation um den Einheitskreis abtastet, ermöglicht die Chirp-Z-Transformation das Abtasten der Z-Transformation entlang jeder logarithmischen Spirale, wie z. B. eines Kreises mit einem Radius kleiner als Eins.

>>> M = fs // 2  # Just positive frequencies, like rfft
>>> a = np.exp(-f1/fs)  # Starting point of the circle, radius < 1
>>> w = np.exp(-1j*np.pi/M)  # "Step size" of circle
>>> points = czt_points(M + 1, w, a)  # M + 1 to include Nyquist
>>> plt.plot(points.real, points.imag, '.')
>>> plt.gca().add_patch(plt.Circle((0,0), radius=1, fill=False, alpha=.3))
>>> plt.axis('equal'); plt.axis([-1.05, 1.05, -0.05, 1.05])
>>> plt.show()

Mit dem richtigen Radius transformiert dies die abfallende Sinuskurve (und andere mit der gleichen Abfallrate) ohne spektrale Leckage

>>> z_vals = czt(x, M + 1, w, a)  # Include Nyquist for comparison to rfft
>>> freqs = np.angle(points)*fs/(2*np.pi)  # angle = omega, radius = sigma
>>> plt.plot(freqs, abs(z_vals))
>>> plt.margins(0, 0.1)
>>> plt.show()