scipy.cluster.hierarchy.

linkage

scipy.cluster.hierarchy.linkage(y, method='single', metric='euclidean', optimal_ordering=False)

Führt hierarchische/agglomerative Clusterbildung durch.

Die Eingabe y kann entweder eine 1D-kondensierte Distanzmatrix oder ein 2D-Array von Beobachtungsvektoren sein.

Wenn y eine 1D-kondensierte Distanzmatrix ist, muss y ein Vektor der Größe \(\binom{n}{2}\) sein, wobei n die Anzahl der ursprünglichen Beobachtungen ist, die in der Distanzmatrix gepaart wurden. Das Verhalten dieser Funktion ist dem der MATLAB-Funktion linkage sehr ähnlich.

Eine Matrix Z der Größe \((n-1)\) mal 4 wird zurückgegeben. In der \(i\)-ten Iteration werden die Cluster mit den Indizes Z[i, 0] und Z[i, 1] kombiniert, um den Cluster \(n + i\) zu bilden. Ein Cluster mit einem Index kleiner als \(n\) entspricht einer der \(n\) ursprünglichen Beobachtungen. Die Distanz zwischen den Clustern Z[i, 0] und Z[i, 1] ist gegeben durch Z[i, 2]. Der vierte Wert Z[i, 3] repräsentiert die Anzahl der ursprünglichen Beobachtungen im neu gebildeten Cluster.

Die folgenden Linkage-Methoden werden verwendet, um die Distanz \(d(s, t)\) zwischen zwei Clustern \(s\) und \(t\) zu berechnen. Der Algorithmus beginnt mit einem Wald von Clustern, die noch nicht im entstehenden Hierarchie verwendet wurden. Wenn zwei Cluster \(s\) und \(t\) aus diesem Wald zu einem einzigen Cluster \(u\) kombiniert werden, werden \(s\) und \(t\) aus dem Wald entfernt und \(u\) wird dem Wald hinzugefügt. Wenn nur noch ein Cluster im Wald verbleibt, stoppt der Algorithmus und dieser Cluster wird zur Wurzel.

In jeder Iteration wird eine Distanzmatrix gepflegt. Der Eintrag d[i,j] entspricht der Distanz zwischen Cluster \(i\) und \(j\) im ursprünglichen Wald.

In jeder Iteration muss der Algorithmus die Distanzmatrix aktualisieren, um die Distanz des neu gebildeten Clusters u zu den verbleibenden Clustern im Wald widerzuspiegeln.

Angenommen, es gibt \(|u|\) ursprüngliche Beobachtungen \(u[0], \ldots, u[|u|-1]\) im Cluster \(u\) und \(|v|\) ursprüngliche Objekte \(v[0], \ldots, v[|v|-1]\) im Cluster \(v\). Zur Erinnerung: \(s\) und \(t\) werden zu Cluster \(u\) kombiniert. Sei \(v\) ein beliebiger verbleibender Cluster im Wald, der nicht \(u\) ist.

Die folgenden Methoden werden zur Berechnung der Distanz zwischen dem neu gebildeten Cluster \(u\) und jedem \(v\) verwendet.

• methode=’single’ weist

  \[d(u,v) = \min(dist(u[i],v[j]))\]

  für alle Punkte \(i\) in Cluster \(u\) und \(j\) in Cluster \(v\). Dies ist auch bekannt als der Algorithmus des nächsten Punktes (Nearest Point Algorithm).

• methode=’complete’ weist

  \[d(u, v) = \max(dist(u[i],v[j]))\]

  für alle Punkte \(i\) in Cluster u und \(j\) in Cluster \(v\). Dies ist auch bekannt als der Algorithmus des entferntesten Punktes (Farthest Point Algorithm) oder Voor Hees Algorithmus.

• methode=’average’ weist

  \[d(u,v) = \sum_{ij} \frac{d(u[i], v[j])} {(|u|*|v|)}\]

  für alle Punkte \(i\) und \(j\), wobei \(|u|\) und \(|v|\) die Kardinalitäten der Cluster \(u\) und \(v\) sind. Dies wird auch als UPGMA-Algorithmus bezeichnet.

• methode=’weighted’ weist

  \[d(u,v) = (dist(s,v) + dist(t,v))/2\]

  wobei Cluster u mit Cluster s und t gebildet wurde und v ein verbleibender Cluster im Wald ist (auch bekannt als WPGMA).

• methode=’centroid’ weist

  \[dist(s,t) = ||c_s-c_t||_2\]

  wobei \(c_s\) und \(c_t\) die Zentroiden der Cluster \(s\) und \(t\) sind. Wenn zwei Cluster \(s\) und \(t\) zu einem neuen Cluster \(u\) kombiniert werden, wird der neue Zentroid über alle ursprünglichen Objekte in den Clustern \(s\) und \(t\) berechnet. Die Distanz wird dann zur euklidischen Distanz zwischen dem Zentroiden von \(u\) und dem Zentroiden eines verbleibenden Clusters \(v\) im Wald.

• methode=’median’ weist \(d(s,t)\) wie die centroid-Methode zu. Wenn zwei Cluster \(s\) und \(t\) zu einem neuen Cluster \(u\) kombiniert werden, ergibt der Durchschnitt der Zentroiden s und t den neuen Zentroiden \(u\). Dies ist auch als WPGMC-Algorithmus bekannt.

• methode=’ward’ verwendet den Ward-Varianzminimierungsalgorithmus. Der neue Eintrag \(d(u,v)\) wird wie folgt berechnet:

  \[d(u,v) = \sqrt{\frac{|v|+|s|} {T}d(v,s)^2 + \frac{|v|+|t|} {T}d(v,t)^2 - \frac{|v|} {T}d(s,t)^2}\]

  wobei \(u\) der neu verbundene Cluster ist, bestehend aus den Clustern \(s\) und \(t\), \(v\) ein ungenutzter Cluster im Wald ist, \(T=|v|+|s|+|t|\) und \(|*|\) die Kardinalität seines Arguments ist. Dies ist auch als inkrementeller Algorithmus bekannt.

Warnung: Wenn das Paar mit der minimalen Distanz im Wald gewählt wird, können zwei oder mehr Paare die gleiche minimale Distanz haben. Diese Implementierung kann eine andere minimale Distanz wählen als die MATLAB-Version.

Parameter:

yndarray

Eine kondensierte Distanzmatrix. Eine kondensierte Distanzmatrix ist ein flacher Array, der die obere Dreiecksmatrix der Distanzmatrix enthält. Dies ist die Form, die pdist zurückgibt. Alternativ kann eine Sammlung von \(m\) Beobachtungsvektoren in \(n\) Dimensionen als Array der Größe \(m \times n\) übergeben werden. Alle Elemente der kondensierten Distanzmatrix müssen endlich sein, d. h. keine NaNs oder Inf.

methodstr, optional

Der zu verwendende Linkage-Algorithmus. Siehe den Abschnitt Linkage-Methoden unten für vollständige Beschreibungen.

metricstr oder Funktion, optional

Die zu verwendende Distanzmetrik, falls y eine Sammlung von Beobachtungsvektoren ist; andernfalls ignoriert. Siehe die Funktion pdist für eine Liste gültiger Distanzmetriken. Eine benutzerdefinierte Distanzfunktion kann ebenfalls verwendet werden.

optimal_orderingbool, optional

Wenn True, wird die Linkage-Matrix neu geordnet, so dass die Distanz zwischen aufeinanderfolgenden Blättern minimal ist. Dies führt zu einer intuitiveren Baumstruktur bei der Visualisierung der Daten. Standardmäßig False, da dieser Algorithmus, insbesondere bei großen Datensätzen, langsam sein kann [2]. Siehe auch die Funktion optimal_leaf_ordering.

Hinzugefügt in Version 1.0.0.

Rückgabe:

Zndarray

Die hierarchische Clusterbildung, kodiert als Linkage-Matrix.

Siehe auch

scipy.spatial.distance.pdist

Paarweise Distanzmetriken

Hinweise

1. Für die Methode ‘single’ wird ein optimierter Algorithmus basierend auf dem Minimalen Spannbaum (Minimum Spanning Tree) implementiert. Dieser hat eine Zeitkomplexität von \(O(n^2)\). Für die Methoden ‘complete’, ‘average’, ‘weighted’ und ‘ward’ wird ein Algorithmus namens Nearest-Neighbors Chain implementiert. Dieser hat ebenfalls eine Zeitkomplexität von \(O(n^2)\). Für andere Methoden wird ein naiver Algorithmus mit \(O(n^3)\) Zeitkomplexität implementiert. Alle Algorithmen verwenden \(O(n^2)\) Speicher. Einzelheiten zu den Algorithmen finden Sie in [1].

2. Die Methoden ‘centroid’, ‘median’ und ‘ward’ sind nur korrekt definiert, wenn die euklidische paarweise Metrik verwendet wird. Wenn y als vorberechnete paarweise Distanzen übergeben wird, liegt es in der Verantwortung des Benutzers, sicherzustellen, dass diese Distanzen tatsächlich euklidisch sind, andernfalls ist das Ergebnis falsch.

linkage verfügt über experimentelle Unterstützung für Python Array API Standard-kompatible Backends zusätzlich zu NumPy. Bitte erwägen Sie, diese Funktionen zu testen, indem Sie die Umgebungsvariable SCIPY_ARRAY_API=1 setzen und CuPy, PyTorch, JAX oder Dask-Arrays als Array-Argumente bereitstellen. Die folgenden Kombinationen von Backend und Gerät (oder anderer Fähigkeit) werden unterstützt.

Bibliothek	CPU	GPU
NumPy	✅	n/a
CuPy	n/a	⛔
PyTorch	✅	⛔
JAX	✅	⛔
Dask	⚠️ führt Chunks zusammen	n/a

Siehe Unterstützung für den Array API Standard für weitere Informationen.

Referenzen

[1]

Daniel Mullner, „Modern hierarchical, agglomerative clustering algorithms“, arXiv:1109.2378v1.

[2]

Ziv Bar-Joseph, David K. Gifford, Tommi S. Jaakkola, „Fast optimal leaf ordering for hierarchical clustering“, 2001. Bioinformatics DOI:10.1093/bioinformatics/17.suppl_1.S22

Beispiele

Probieren Sie es in Ihrem Browser aus!

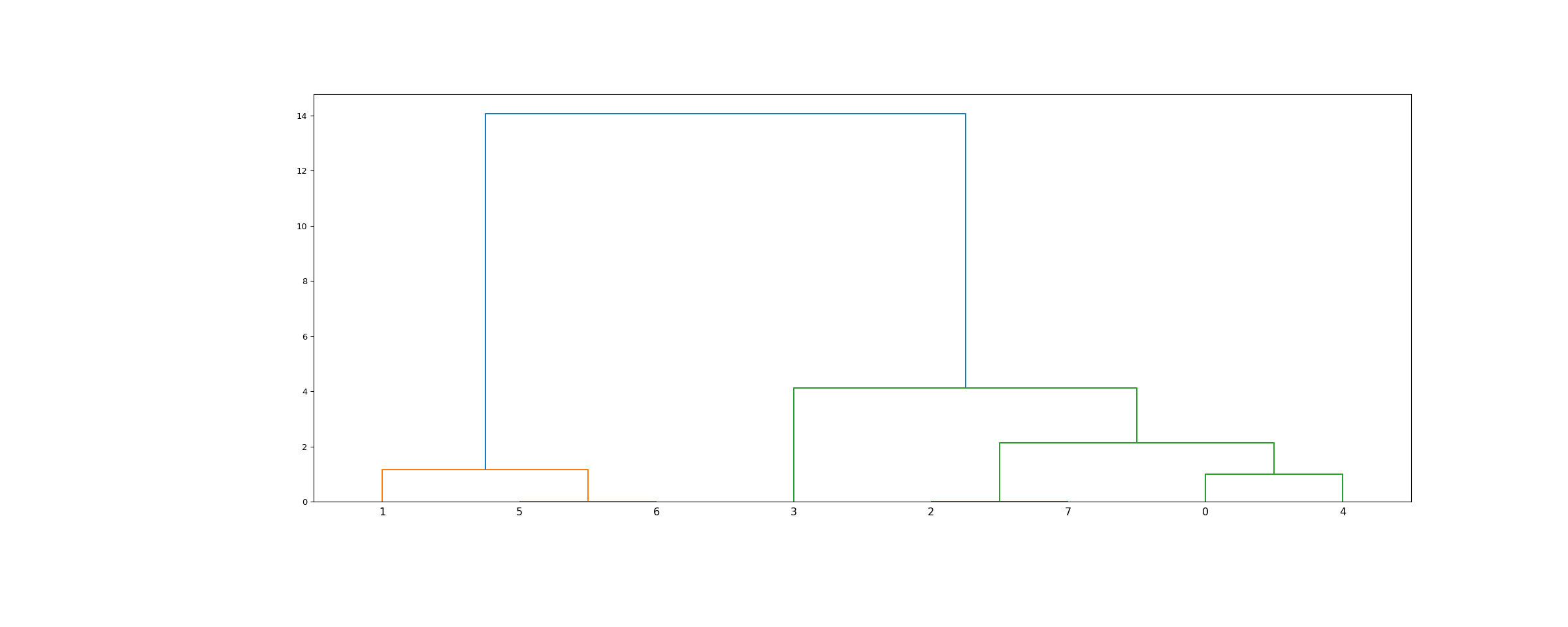
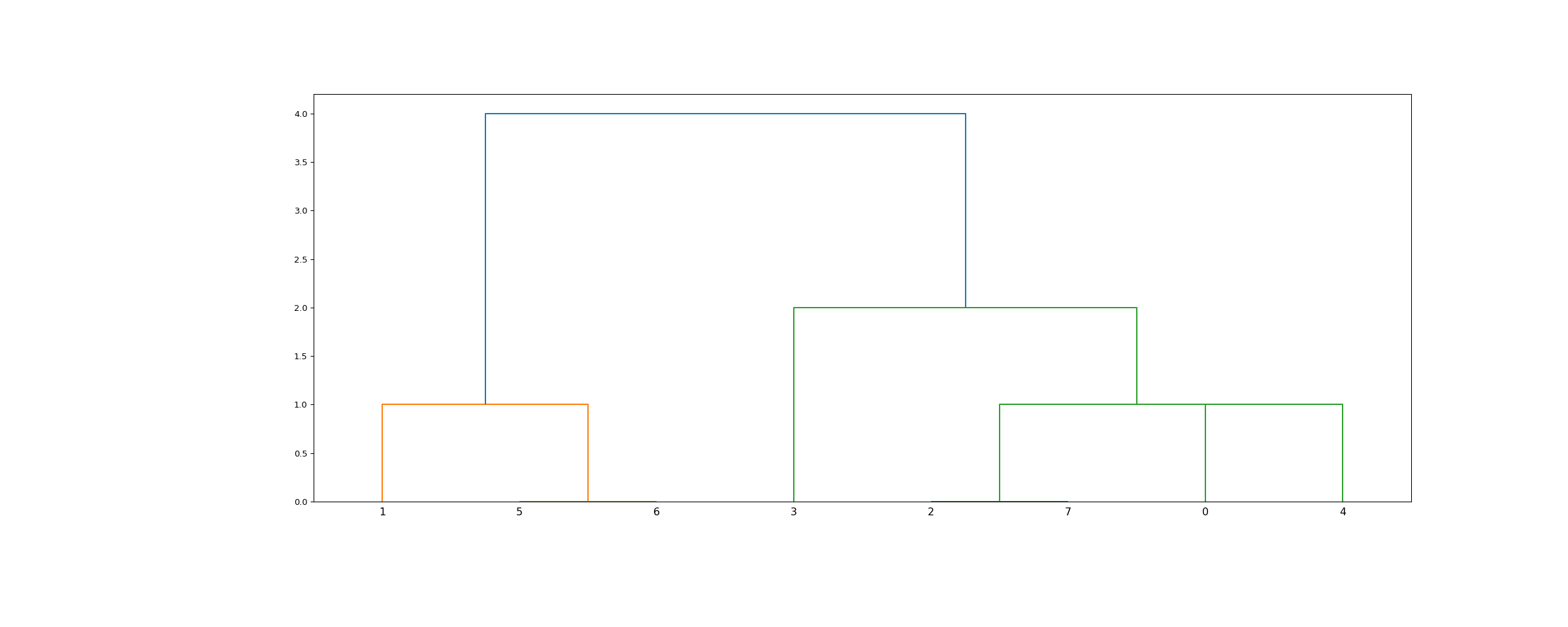
>>> from scipy.cluster.hierarchy import dendrogram, linkage
>>> from matplotlib import pyplot as plt
>>> X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]]

>>> Z = linkage(X, 'ward')
>>> fig = plt.figure(figsize=(25, 10))
>>> dn = dendrogram(Z)

>>> Z = linkage(X, 'single')
>>> fig = plt.figure(figsize=(25, 10))
>>> dn = dendrogram(Z)
>>> plt.show()

ZurückIn Tab öffnen