scipy.integrate.

lebedev_rule#

scipy.integrate.lebedev_rule(n)[Quelle]#

Lebedev-Quadratur.

Berechnet die Abtastpunkte und Gewichte für die Lebedev-Quadratur [1] zur Integration einer Funktion über die Oberfläche einer Einheitskugel.

Parameter:

nint: Ordnung der Quadratur. Unterstützte Werte siehe Hinweise.

Rückgabe:

xndarray der Form (3, m): Abtastpunkte auf der Einheitskugel in kartesischen Koordinaten. m ist der "Grad", der der angegebenen Ordnung entspricht; siehe Hinweise.
wndarray der Form (m,): Gewichte

Hinweise

Implementiert durch Übersetzung des Matlab-Codes von [2] nach Python.

Die verfügbaren Ordnungen (Argument n) sind

3, 5, 7, 9, 11, 13, 15, 17,
19, 21, 23, 25, 27, 29, 31, 35,
41, 47, 53, 59, 65, 71, 77, 83,
89, 95, 101, 107, 113, 119, 125, 131

Die entsprechenden Grade m sind

6, 14, 26, 38, 50, 74, 86, 110,
146, 170, 194, 230, 266, 302, 350, 434,
590, 770, 974, 1202, 1454, 1730, 2030, 2354,
2702, 3074, 3470, 3890, 4334, 4802, 5294, 5810

Referenzen

[1]

V.I. Lebedev und D.N. Laikov. „A quadrature formula for the sphere of the 131st algebraic order of accuracy“. Doklady Mathematics, Bd. 59, Nr. 3, 1999, S. 477-481.

[2]

R. Parrish. getLebedevSphere. Matlab Central File Exchange. https://www.mathworks.com/matlabcentral/fileexchange/27097-getlebedevsphere.

[3]

Bellet, Jean-Baptiste, Matthieu Brachet und Jean-Pierre Croisille. „Quadrature and symmetry on the Cubed Sphere.“ Journal of Computational and Applied Mathematics 409 (2022): 114142. DOI:10.1016/j.cam.2022.114142.

Beispiele

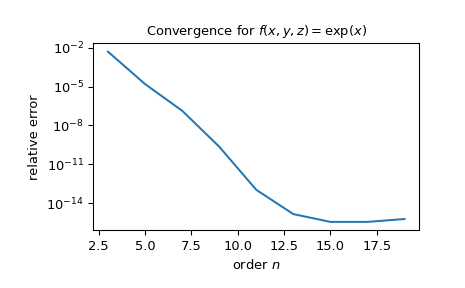
Ein Beispiel, das in [3] gegeben wird, ist die Integration von \(f(x, y, z) = \exp(x)\) über eine Kugel mit dem Radius \(1\); die Referenz dort ist 14.7680137457653. Zeigen Sie die Konvergenz zum erwarteten Ergebnis mit zunehmender Ordnung.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.integrate import lebedev_rule
>>>
>>> def f(x):
...     return np.exp(x[0])
>>>
>>> res = []
>>> orders = np.arange(3, 20, 2)
>>> for n in orders:
...     x, w = lebedev_rule(n)
...     res.append(w @ f(x))
>>>
>>> ref = np.full_like(res, 14.7680137457653)
>>> err = abs(res - ref)/abs(ref)
>>> plt.semilogy(orders, err)
>>> plt.xlabel('order $n$')
>>> plt.ylabel('relative error')
>>> plt.title(r'Convergence for $f(x, y, z) = \exp(x)$')
>>> plt.show()

../../_images/scipy-integrate-lebedev_rule-1.png