Akima1DInterpolator#
- class scipy.interpolate.Akima1DInterpolator(x, y, axis=0, *, method='akima', extrapolate=None)[Quelle]#
Akima „visuell ansprechender“ Interpolator (C1 glatt).
Passen Sie stückweise kubische Polynome an, gegeben durch die Vektoren x und y. Die Interpolationsmethode von Akima verwendet eine kontinuierlich differenzierbare Sub-Spline, die aus stückweisen kubischen Polynomen aufgebaut ist. Die resultierende Kurve verläuft durch die gegebenen Datenpunkte und erscheint glatt und natürlich.
- Parameter:
- xndarray, Form (npoints, )
1-D-Array von monoton steigenden reellen Werten.
- yndarray, Form (…, npoints, …)
N-D-Array von reellen Werten. Die Länge von
yentlang der Interpolationsachse muss gleich der Länge vonxsein. Verwenden Sie den Parameteraxis, um die Interpolationsachse auszuwählen.- axisint, optional
Achse im
y-Array, die den x-Koordinatenwerten entspricht. Standardmäßigaxis=0.- method{‘akima’, ‘makima’}, optional
Wenn
"makima", verwenden Sie die modifizierte Akima-Interpolation [2]. Standardmäßig"akima", verwenden Sie die Akima-Interpolation [1].Hinzugefügt in Version 1.13.0.
- extrapolate{bool, None}, optional
Wenn bool, bestimmt, ob für Punkte außerhalb des Bereichs basierend auf dem ersten und letzten Intervall extrapoliert oder NaNs zurückgegeben werden sollen. Wenn None, wird
extrapolateauf False gesetzt.
- Attribute:
- axis
- c
- extrapolate
- x
Methoden
__call__(x[, nu, extrapolate])Evaluiere das stückweise definierte Polynom oder seine Ableitung.
derivative([nu])Erstelle ein neues stückweise definiertes Polynom, das die Ableitung darstellt.
antiderivative([nu])Erstelle ein neues stückweise definiertes Polynom, das die Stammfunktion darstellt.
integrate(a, b[, extrapolate])Berechne ein bestimmtes Integral über ein stückweise definiertes Polynom.
solve([y, discontinuity, extrapolate])Findet reelle Lösungen der Gleichung
pp(x) == y.roots([discontinuity, extrapolate])Reelle Wurzeln des stückweisen Polynoms finden.
Siehe auch
PchipInterpolatorPCHIP 1D monotoiner kubischer Interpolator.
CubicSplineKubischer Spline-Dateninterpolator.
PPolyStückweises Polynom in Bezug auf Koeffizienten und Bruchstellen
Hinweise
Hinzugefügt in Version 0.14.
Nur für präzise Daten verwenden, da die angepasste Kurve exakt durch die gegebenen Punkte verläuft. Diese Routine ist nützlich, um eine angenehm glatte Kurve durch wenige gegebene Punkte zu zeichnen.
Sei \(\delta_i = (y_{i+1} - y_i) / (x_{i+1} - x_i)\) die Steigung des Intervalls \(\left[x_i, x_{i+1}\right)\). Die Ableitung von Akima bei \(x_i\) ist definiert als
\[d_i = \frac{w_1}{w_1 + w_2}\delta_{i-1} + \frac{w_2}{w_1 + w_2}\delta_i\]In der Akima-Interpolation [1] (
method="akima") sind die Gewichte\[\begin{split}\begin{aligned} w_1 &= |\delta_{i+1} - \delta_i| \\ w_2 &= |\delta_{i-1} - \delta_{i-2}| \end{aligned}\end{split}\]In der modifizierten Akima-Interpolation [2] (
method="makima"), um Überschwingen zu vermeiden und Ausnahmefälle zu vermeiden, in denen sowohl Zähler als auch Nenner gleich 0 sind, werden die Gewichte wie folgt modifiziert:\[\begin{split}\begin{align*} w_1 &= |\delta_{i+1} - \delta_i| + |\delta_{i+1} + \delta_i| / 2 \\ w_2 &= |\delta_{i-1} - \delta_{i-2}| + |\delta_{i-1} + \delta_{i-2}| / 2 \end{align*}\end{split}\]Referenzen
[1] (1,2)Ein neues Verfahren zur Interpolation und glatten Kurvenanpassung basierend auf lokalen Verfahren. Hiroshi Akima, J. ACM, Oktober 1970, 17(4), 589-602. DOI:10.1145/321607.321609
[2] (1,2)Makima Stückweise kubische Interpolation. Cleve Moler und Cosmin Ionita, 2019. https://blogs.mathworks.com/cleve/2019/04/29/makima-piecewise-cubic-interpolation/
Beispiele
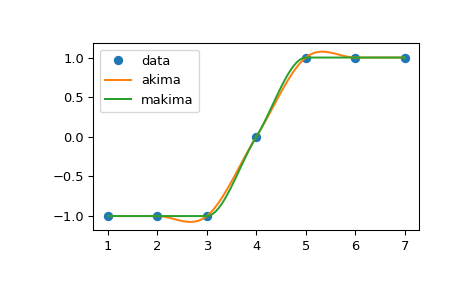
Vergleich von
method="akima"undmethod="makima">>> import numpy as np >>> from scipy.interpolate import Akima1DInterpolator >>> import matplotlib.pyplot as plt >>> x = np.linspace(1, 7, 7) >>> y = np.array([-1, -1, -1, 0, 1, 1, 1]) >>> xs = np.linspace(min(x), max(x), num=100) >>> y_akima = Akima1DInterpolator(x, y, method="akima")(xs) >>> y_makima = Akima1DInterpolator(x, y, method="makima")(xs)
>>> fig, ax = plt.subplots() >>> ax.plot(x, y, "o", label="data") >>> ax.plot(xs, y_akima, label="akima") >>> ax.plot(xs, y_makima, label="makima") >>> ax.legend() >>> fig.show()
Das Überschwingen, das bei
"akima"auftrat, wurde bei"makima"vermieden.