scipy.interpolate.BSpline.

basis_element

classmethod BSpline.basis_element(t, extrapolate=True)

Gibt ein B-Spline-Basiselement B(x | t[0], ..., t[k+1]) zurück.

Parameter:

tndarray, Form (k+2,)

interne Knoten

extrapolatebool oder ‘periodic’, optional

ob über das Basisintervall, t[0] .. t[k+1], hinaus extrapoliert werden soll oder ob NaNs zurückgegeben werden sollen. Wenn ‘periodic’, wird periodische Extrapolation verwendet. Standard ist True.

Rückgabe:

basis_elementcallable

Ein aufrufbares Objekt, das ein B-Spline-Basiselement für den Knotenvektor t repräsentiert.

Hinweise

Der Grad des B-Splines, k, wird aus der Länge von t als len(t)-2 abgeleitet. Der Knotenvektor wird konstruiert, indem k+1 Elemente an die internen Knoten t angehängt und vorangestellt werden.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Konstruieren eines kubischen B-Splines

>>> import numpy as np
>>> from scipy.interpolate import BSpline
>>> b = BSpline.basis_element([0, 1, 2, 3, 4])
>>> k = b.k
>>> b.t[k:-k]
array([ 0.,  1.,  2.,  3.,  4.])
>>> k
3

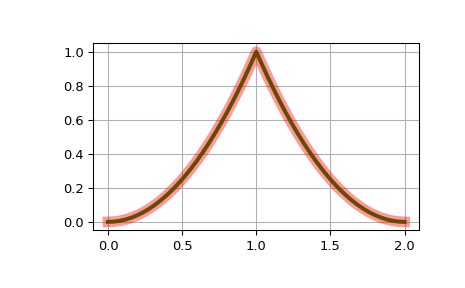
Konstruieren eines quadratischen B-Splines auf [0, 1, 1, 2] und Vergleichen mit seiner expliziten Form

>>> t = [0, 1, 1, 2]
>>> b = BSpline.basis_element(t)
>>> def f(x):
...     return np.where(x < 1, x*x, (2. - x)**2)

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(0, 2, 51)
>>> ax.plot(x, b(x), 'g', lw=3)
>>> ax.plot(x, f(x), 'r', lw=8, alpha=0.4)
>>> ax.grid(True)
>>> plt.show()

ZurückIn Tab öffnen