scipy.interpolate.

FloaterHormannInterpolator

class scipy.interpolate.FloaterHormannInterpolator(points, values, *, d=3)

Floater-Hormann baryzentrischer rationaler Interpolator (C∞ glatt auf der reellen Achse).

Wie in [1] beschrieben, berechnet die Methode von Floater und Hormann Gewichte für einen baryzentrischen rationalen Interpolanten ohne Pole auf der reellen Achse.

Parameter:

x1D Array_like, Form (n,)

1D-Array, das die Werte der unabhängigen Variablen enthält. Werte können reell oder komplex, müssen aber endlich sein.

yarray_like, Form (n, …)

Array, das die Werte der abhängigen Variablen enthält. Unendliche und NaN-Werte von y und entsprechende Werte von x werden verworfen.

dint, Standardwert: 3

Ganzzahl, die 0 <= d < n erfüllt. Die Floater-Hormann-Interpolation mischt n - d Polynome vom Grad d zusammen; für d = n - 1 ist dies äquivalent zur Polynominterpolation.

Attribute:

weightsarray

Gewichte der baryzentrischen Approximation.

Methoden

__call__(z)	Evaluiert die rationale Approximation an gegebenen Werten.
poles()	Berechnet die Pole der rationalen Approximation.
residues()	Berechnet die Residuen der Pole der Approximation.
roots()	Berechnet die Nullstellen der rationalen Approximation.

Siehe auch

AAA

Baryzentrische rationale Approximation von reellen und komplexen Funktionen.

pade

Padé-Approximation.

Hinweise

Der Floater-Hormann-Interpolant ist eine rationale Funktion, die die Daten mit einer Approximationsordnung von \(O(h^{d+1})\) interpoliert. Die rationale Funktion mischt n - d Polynome vom Grad d zusammen, um einen rationalen Interpolanten zu erzeugen, der im Gegensatz zu AAA keine Pole auf der reellen Achse aufweist. Der Interpolant ist gegeben durch

\[r(x) = \frac{\sum_{i=0}^{n-d} \lambda_i(x) p_i(x)} {\sum_{i=0}^{n-d} \lambda_i(x)},\]

wobei \(p_i(x)\) ein interpolierendes Polynom von höchstens Grad d durch die Punkte \((x_i,y_i),\dots,(x_{i+d},y_{i+d})\) ist und \(\lambda_i(z)\) die Mischfunktionen sind, die definiert sind durch

\[\lambda_i(x) = \frac{(-1)^i}{(x - x_i)\cdots(x - x_{i+d})}.\]

Wenn d = n - 1 ist, reduziert sich dies auf Polynominterpolation.

Aufgrund seiner Stabilität wird die folgende baryzentrische Darstellung der obigen Gleichung für die Berechnung verwendet

\[r(z) = \frac{\sum_{k=1}^m\ w_k f_k / (x - x_k)}{\sum_{k=1}^m w_k / (x - x_k)},\]

wobei die Gewichte \(w_j\) wie folgt berechnet werden

\[\begin{split}w_k &= (-1)^{k - d} \sum_{i \in J_k} \prod_{j = i, j \neq k}^{i + d} 1/|x_k - x_j|, \\ J_k &= \{ i \in I: k - d \leq i \leq k\},\\ I &= \{0, 1, \dots, n - d\}.\end{split}\]

Referenzen

[1]

M.S. Floater und K. Hormann, „Barycentric rational interpolation with no poles and high rates of approximation“, Numer. Math. 107, 315 (2007). DOI:10.1007/s00211-007-0093-y

Beispiele

Probieren Sie es in Ihrem Browser aus!

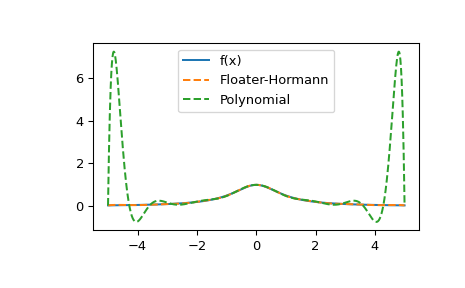
Hier vergleichen wir die Methode mit der Polynominterpolation anhand eines Beispiels, bei dem die Polynominterpolation aufgrund des Runge-Phänomens fehlschlägt.

>>> import numpy as np
>>> from scipy.interpolate import (FloaterHormannInterpolator,
...                                BarycentricInterpolator)
>>> def f(x):
...     return 1/(1 + x**2)
>>> x = np.linspace(-5, 5, num=15)
>>> r = FloaterHormannInterpolator(x, f(x))
>>> p = BarycentricInterpolator(x, f(x))
>>> xx = np.linspace(-5, 5, num=1000)
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> ax.plot(xx, f(xx), label="f(x)")
>>> ax.plot(xx, r(xx), "--", label="Floater-Hormann")
>>> ax.plot(xx, p(xx), "--", label="Polynomial")
>>> ax.legend()
>>> plt.show()

ZurückIn Tab öffnen