RegularGridInterpolator#
- class scipy.interpolate.RegularGridInterpolator(points, values, method='linear', bounds_error=True, fill_value=nan, *, solver=None, solver_args=None)[Quelle]#
Interpolator der angegebenen Ordnung auf einem rechtwinkligen Gitter in N ≥ 1 Dimensionen.
Die Daten müssen auf einem rechtwinkligen Gitter definiert sein; das heißt, einem rechteckigen Gitter mit gleichmäßigen oder ungleichmäßigen Abständen. Lineare, Nächste-Nachbar- und Spline-Interpolationen werden unterstützt. Nach der Einrichtung des Interpolator-Objekts kann die Interpolationsmethode bei jeder Auswertung gewählt werden.
- Parameter:
- pointstuple von ndarray von float, mit Formen (m1, ), …, (mn, )
Die Punkte, die das regelmäßige Gitter in n Dimensionen definieren. Die Punkte in jeder Dimension (d.h. jedes Element des points-Tupels) müssen streng aufsteigend oder absteigend sein.
- valuesarray_like, Form (m1, …, mn, …)
Die Daten auf dem regelmäßigen Gitter in n Dimensionen. Komplexe Daten sind zulässig.
- methodstr, optional
Die durchzuführende Interpolationsmethode. Unterstützt werden „linear“, „nearest“, „slinear“, „cubic“, „quintic“ und „pchip“. Dieser Parameter wird zum Standard für die
__call__-Methode des Objekts.- bounds_errorbool, optional
Wenn True, wird ein ValueError ausgelöst, wenn interpolierte Werte außerhalb des Bereichs der Eingabedaten angefordert werden. Wenn False, wird fill_value verwendet. Standard ist True.
- fill_valuefloat oder None, optional
Der Wert, der für Punkte außerhalb des Interpolationsbereichs verwendet wird. Wenn None, werden Werte außerhalb des Bereichs extrapoliert. Standard ist
np.nan.- solvercallable, optional
Nur verwendet für die Methoden „slinear“, „cubic“ und „quintic“. Sparse Löser für die Konstruktion der NdBSpline-Instanz. Standard ist der iterative Löser
scipy.sparse.linalg.gcrotmk.Hinzugefügt in Version 1.13.
- solver_args: dict, optional
Zusätzliche Argumente, die an solver übergeben werden, falls vorhanden.
Hinzugefügt in Version 1.13.
- Attribute:
- gridtuple von ndarrays
Die Punkte, die das regelmäßige Gitter in n Dimensionen definieren. Dieses Tupel definiert das vollständige Gitter über
np.meshgrid(*grid, indexing='ij')- valuesndarray
Datenwerte am Gitter.
- methodstr
Interpolationsmethode.
- fill_valuefloat oder
None Verwenden Sie diesen Wert für Argumente außerhalb des Bereichs an
__call__.- bounds_errorbool
Wenn
True, lösen Argumente außerhalb des Bereichs einenValueErroraus.
Methoden
__call__(xi[, method, nu])Interpolation an Koordinaten.
Siehe auch
NearestNDInterpolatorNächste-Nachbar-Interpolator auf *unstrukturierten* Daten in N Dimensionen
LinearNDInterpolatorStückweise linearer Interpolator auf *unstrukturierten* Daten in N Dimensionen
interpneine Hilfsfunktion, die
RegularGridInterpolatorumschließtscipy.ndimage.map_coordinatesInterpolation auf Gittern mit gleichem Abstand (geeignet für z.B. N-dimensionale Bild-Resampling)
Hinweise
Im Gegensatz zu
LinearNDInterpolatorundNearestNDInterpolatorvermeidet diese Klasse eine teure Triangulierung der Eingabedaten, indem sie die Struktur des regelmäßigen Gitters ausnutzt.Mit anderen Worten, diese Klasse geht davon aus, dass die Daten auf einem *rechtwinkligen* Gitter definiert sind.
Hinzugefügt in Version 0.14.
Die Methoden „slinear“(k=1), „cubic“(k=3) und „quintic“(k=5) sind Tensorprodukt-Spline-Interpolatoren, wobei k der Grad des Splines ist. Wenn eine Dimension weniger als k + 1 Punkte hat, wird ein Fehler ausgelöst.
Hinzugefügt in Version 1.9.
Wenn die Eingabedaten so beschaffen sind, dass die Dimensionen inkonsistente Einheiten haben und sich um viele Größenordnungen unterscheiden, kann der Interpolant numerische Artefakte aufweisen. Erwägen Sie die Skalierung der Daten vor der Interpolation.
Auswahl eines Solvers für Spline-Methoden
Spline-Methoden, „slinear“, „cubic“ und „quintic“ beinhalten das Lösen eines großen dünnbesetzten linearen Systems zur Instanziierungszeit. Je nach Daten kann der Standard-Solver ausreichend sein oder auch nicht. Wenn er nicht ausreichend ist, müssen Sie möglicherweise mit einem optionalen solver-Argument experimentieren, wobei Sie zwischen dem direkten Solver (
scipy.sparse.linalg.spsolve) oder iterativen Lösern ausscipy.sparse.linalgwählen können. Möglicherweise müssen Sie zusätzliche Parameter über den optionalen solver_args-Parameter angeben (z.B. den Startwert oder die Zieltoleranz). Sehen Sie in der Dokumentation vonscipy.sparse.linalgnach der vollständigen Liste der verfügbaren Optionen.Alternativ können Sie auch die Legacy-Methoden „slinear_legacy“, „cubic_legacy“ und „quintic_legacy“ verwenden. Diese Methoden ermöglichen eine schnellere Konstruktion, die Auswertung wird jedoch viel langsamer sein.
Rundungsregel an halben Punkten bei der Methode `nearest`
Die Rundungsregel bei der Methode nearest an halben Punkten ist das Abrunden.
Referenzen
[1]Python-Paket *regulargrid* von Johannes Buchner, siehe https://pypi.python.org/pypi/regulargrid/
[2]Wikipedia, „Trilineare Interpolation“, https://en.wikipedia.org/wiki/Trilinear_interpolation
[3]Weiser, Alan und Sergio E. Zarantonello. „A note on piecewise linear and multilinear table interpolation in many dimensions.“ MATH. COMPUT. 50.181 (1988): 189-196. https://www.ams.org/journals/mcom/1988-50-181/S0025-5718-1988-0917826-0/S0025-5718-1988-0917826-0.pdf DOI:10.1090/S0025-5718-1988-0917826-0
Beispiele
Evaluieren einer Funktion an den Punkten eines 3D-Gitters
Als erstes Beispiel werten wir eine einfache Beispiel-Funktion an den Punkten eines 3D-Gitters aus
>>> from scipy.interpolate import RegularGridInterpolator >>> import numpy as np >>> def f(x, y, z): ... return 2 * x**3 + 3 * y**2 - z >>> x = np.linspace(1, 4, 11) >>> y = np.linspace(4, 7, 22) >>> z = np.linspace(7, 9, 33) >>> xg, yg ,zg = np.meshgrid(x, y, z, indexing='ij', sparse=True) >>> data = f(xg, yg, zg)
dataist nun ein 3D-Array mitdata[i, j, k] = f(x[i], y[j], z[k]). Als Nächstes definieren wir eine interpolierende Funktion aus diesen Daten>>> interp = RegularGridInterpolator((x, y, z), data)
Werten Sie die interpolierende Funktion an den beiden Punkten
(x,y,z) = (2.1, 6.2, 8.3)und(3.3, 5.2, 7.1)aus>>> pts = np.array([[2.1, 6.2, 8.3], ... [3.3, 5.2, 7.1]]) >>> interp(pts) array([ 125.80469388, 146.30069388])
was tatsächlich eine gute Annäherung an
>>> f(2.1, 6.2, 8.3), f(3.3, 5.2, 7.1) (125.54200000000002, 145.894)
Interpolation und Extrapolation eines 2D-Datensatzes
Als zweites Beispiel interpolieren und extrapolieren wir einen 2D-Datensatz
>>> x, y = np.array([-2, 0, 4]), np.array([-2, 0, 2, 5]) >>> def ff(x, y): ... return x**2 + y**2
>>> xg, yg = np.meshgrid(x, y, indexing='ij') >>> data = ff(xg, yg) >>> interp = RegularGridInterpolator((x, y), data, ... bounds_error=False, fill_value=None)
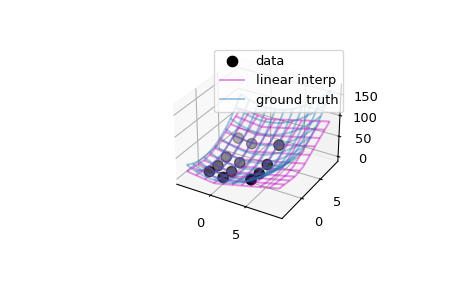
>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax = fig.add_subplot(projection='3d') >>> ax.scatter(xg.ravel(), yg.ravel(), data.ravel(), ... s=60, c='k', label='data')
Werten Sie den Interpolator auf einem feineren Gitter aus und plotten Sie ihn
>>> xx = np.linspace(-4, 9, 31) >>> yy = np.linspace(-4, 9, 31) >>> X, Y = np.meshgrid(xx, yy, indexing='ij')
>>> # interpolator >>> ax.plot_wireframe(X, Y, interp((X, Y)), rstride=3, cstride=3, ... alpha=0.4, color='m', label='linear interp')
>>> # ground truth >>> ax.plot_wireframe(X, Y, ff(X, Y), rstride=3, cstride=3, ... alpha=0.4, label='ground truth') >>> plt.legend() >>> plt.show()
Weitere Beispiele finden Sie im Tutorial.