scipy.interpolate.

generate_knots#

scipy.interpolate.generate_knots(x, y, *, w=None, xb=None, xe=None, k=3, s=0, nest=None)[Quelle]#

Generiert Knotenvektoren, bis das Least-Squares (LSQ)-Kriterium erfüllt ist.

Parameter:

x, yarray_like: Die Datenpunkte, die die Kurve y = f(x) definieren.
warray_like, optional: Gewichte.
xbfloat, optional: Die Grenze des Approximationsintervalls. Wenn None (Standard), wird es auf x[0] gesetzt.
xefloat, optional: Die Grenze des Approximationsintervalls. Wenn None (Standard), wird es auf x[-1] gesetzt.
kint, optional: Der Grad der Spline. Standard ist kubisch, k = 3.
sfloat, optional: Der Glättungsfaktor. Standard ist s = 0.
nestint, optional: Stoppt, wenn mindestens so viele Knoten platziert sind.

Erzeugt:

tndarray: Knotenvektoren mit zunehmender Anzahl von Knoten. Der Generator ist endlich: er stoppt, wenn das Glättungskriterium erfüllt ist oder wenn die Anzahl der Knoten den Maximalwert überschreitet: den vom Benutzer bereitgestellten nest oder x.size + k + 1 – was der Knotenvektor für die interpolierende Spline ist.

Hinweise

Die Routine generiert aufeinanderfolgende Knotenvektoren zunehmender Länge, beginnend bei 2*(k+1) bis len(x) + k + 1, und versucht, die Knoten in den Regionen dichter zu machen, in denen die Abweichung der LSQ-Spline von den Daten groß ist.

Wenn die maximale Anzahl von Knoten erreicht ist (len(x) + k + 1) (dies geschieht, wenn s klein und nest groß ist), stoppt der Generator und die letzte Ausgabe sind die Knoten für die Interpolation mit der Not-a-Knot-Randbedingung.

Knoten werden an Datenstellen platziert, es sei denn, k ist gerade und die Anzahl der Knoten ist len(x) + k + 1. In diesem Fall hat die letzte Ausgabe des Generators interne Knoten an Greville-Stellen, (x[1:] + x[:-1]) / 2.

Hinzugefügt in Version 1.15.0.

Beispiele

Generiert einige verrauschte Daten und passt eine Sequenz von LSQ-Splines an.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import make_lsq_spline, generate_knots
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(size=50)

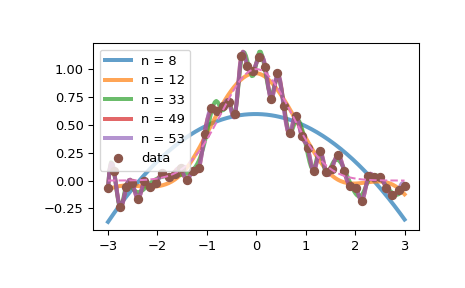
>>> knots = list(generate_knots(x, y, s=1e-10))
>>> for t in knots[::3]:
...     spl = make_lsq_spline(x, y, t)
...     xs = xs = np.linspace(-3, 3, 201)
...     plt.plot(xs, spl(xs), '-', label=f'n = {len(t)}', lw=3, alpha=0.7)
>>> plt.plot(x, y, 'o', label='data')
>>> plt.plot(xs, np.exp(-xs**2), '--')
>>> plt.legend()

Beachten Sie, dass die Erhöhung der Anzahl von Knoten dazu führt, dass das Ergebnis die Daten immer genauer verfolgt.

Beachten Sie auch, dass ein Schritt des Generators mehrere Knoten hinzufügen kann.

>>> [len(t) for t in knots]
[8, 9, 10, 12, 16, 24, 40, 48, 52, 54]

../../_images/scipy-interpolate-generate_knots-1.png