krogh_interpolate#
- scipy.interpolate.krogh_interpolate(xi, yi, x, der=0, axis=0)[Quelle]#
Bequeme Funktion für die Krogh-Interpolation.
Weitere Details finden Sie unter
KroghInterpolator.- Parameter:
- xiarray_like
Interpolationspunkte (bekannte x-Koordinaten).
- yiarray_like
Bekannte y-Koordinaten, mit der Form
(xi.size, R). Interpretiert als Vektoren der Länge R oder Skalare, wenn R=1.- xarray_like
Punkt oder Punkte, an denen die Ableitungen ausgewertet werden sollen.
- derint oder list oder None, optional
Wie viele Ableitungen ausgewertet werden sollen, oder None für alle potenziell nicht-null Ableitungen (d. h. eine Zahl gleich der Anzahl der Punkte) oder eine Liste der auszuwertenden Ableitungen. Diese Zahl enthält den Funktionswert als '0-te' Ableitung.
- axisint, optional
Achse im yi-Array, die den x-Koordinatenwerten entspricht.
- Rückgabe:
- dndarray
Wenn die Werte des Interpolators 2D sind, dann hat das zurückgegebene Array die Form Anzahl der Ableitungen mal N mal R. Wenn x ein Skalar ist, wird die mittlere Dimension weggelassen; wenn yi Skalare sind, wird die letzte Dimension weggelassen.
Siehe auch
KroghInterpolatorKrogh-Interpolationsfunktion
Hinweise
Die Konstruktion des interpolierenden Polynoms ist ein relativ teurer Prozess. Wenn Sie es wiederholt auswerten möchten, sollten Sie die Klasse KroghInterpolator verwenden (die diese Funktion verwendet).
Beispiele
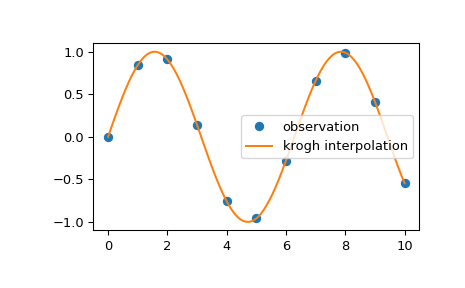
Wir können 2D-beobachtete Daten mit Krogh-Interpolation interpolieren
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.interpolate import krogh_interpolate >>> x_observed = np.linspace(0.0, 10.0, 11) >>> y_observed = np.sin(x_observed) >>> x = np.linspace(min(x_observed), max(x_observed), num=100) >>> y = krogh_interpolate(x_observed, y_observed, x) >>> plt.plot(x_observed, y_observed, "o", label="observation") >>> plt.plot(x, y, label="krogh interpolation") >>> plt.legend() >>> plt.show()