scipy.optimize.

least_squares#

scipy.optimize.least_squares(fun, x0, jac='2-point', bounds=(-inf, inf), method='trf', ftol=1e-08, xtol=1e-08, gtol=1e-08, x_scale=None, loss='linear', f_scale=1.0, diff_step=None, tr_solver=None, tr_options=None, jac_sparsity=None, max_nfev=None, verbose=0, args=(), kwargs=None, callback=None, workers=None)[Quelle]#

Löst ein nichtlineares Kleinste-Quadrate-Problem mit Variablenbeschränkungen.

Gegeben die Residuen f(x) (eine m-dimensionale reelle Funktion von n reellen Variablen) und die Verlustfunktion rho(s) (eine skalare Funktion), findet least_squares ein lokales Minimum der Kostenfunktion F(x)

minimize F(x) = 0.5 * sum(rho(f_i(x)**2), i = 0, ..., m - 1)
subject to lb <= x <= ub

Der Zweck der Verlustfunktion rho(s) ist es, den Einfluss von Ausreißern auf die Lösung zu reduzieren.

Parameter:

funcallable

Funktion, die den Residuenvektor berechnet, mit der Signatur fun(x, *args, **kwargs), d.h. die Minimierung erfolgt in Bezug auf ihr erstes Argument. Das an diese Funktion übergebene Argument x ist ein ndarray der Form (n,) (nie ein Skalar, auch nicht für n=1). Sie muss ein eindimensionales Array_like der Form (m,) oder einen Skalar zuweisen und zurückgeben. Wenn das Argument x komplex ist oder die Funktion fun komplexe Residuen zurückgibt, muss sie in eine reelle Funktion reeller Argumente eingekapselt werden, wie am Ende des Beispielabschnitts gezeigt.

x0array_like mit Form (n,) oder float

Anfangsschätzung für die unabhängigen Variablen. Wenn float, wird sie als 1D-Array mit einem Element behandelt. Wenn method 'trf' ist, kann die Anfangsschätzung leicht angepasst werden, um ausreichend innerhalb der gegebenen bounds zu liegen.

jac{‘2-point’, ‘3-point’, ‘cs’, callable}, optional

Methode zur Berechnung der Jacobi-Matrix (eine m-mal-n-Matrix, wobei das Element (i, j) die partielle Ableitung von f[i] nach x[j] ist). Die Schlüsselwörter wählen ein Differenzenverfahren zur numerischen Schätzung. Das Verfahren '3-point' ist genauer, erfordert aber doppelt so viele Operationen wie '2-point' (Standard). Das Verfahren 'cs' verwendet komplexe Schritte und ist, obwohl potenziell am genauesten, nur anwendbar, wenn fun komplexe Eingaben korrekt behandelt und analytisch auf die komplexe Ebene fortgesetzt werden kann. Wenn callable, wird es als jac(x, *args, **kwargs) verwendet und sollte eine gute Annäherung (oder den exakten Wert) der Jacobi-Matrix als Array_like (np.atleast_2d wird angewendet), ein Sparse-Array (csr_array für bessere Leistung bevorzugt) oder einen scipy.sparse.linalg.LinearOperator zurückgeben.

Geändert in Version 1.16.0: Die Möglichkeit, die Schlüsselwörter '3-point', 'cs' mit der Methode 'lm' zu verwenden. Zuvor war 'lm' auf '2-point' und callable beschränkt.

bounds2-Tupel aus array_like oder Bounds, optional

Es gibt zwei Möglichkeiten, Grenzen anzugeben

Instanz der Klasse Bounds
Untere und obere Grenzen für die unabhängigen Variablen. Standardmäßig keine Grenzen. Jedes Array muss die Größe von x0 haben oder ein Skalar sein, in letzterem Fall ist eine Grenze für alle Variablen gleich. Verwenden Sie np.inf mit dem entsprechenden Vorzeichen, um Grenzen für alle oder einige Variablen zu deaktivieren.

method{‘trf’, ‘dogbox’, ‘lm’}, optional

Algorithmus zur Durchführung der Minimierung.

‘trf’ : Trust Region Reflective Algorithmus, besonders geeignet für große dünn besetzte Probleme mit Beschränkungen. Generell ein robuster Algorithmus.
‘dogbox’ : Dogleg-Algorithmus mit rechteckigen Trust-Regionen, typischer Anwendungsfall sind kleine Probleme mit Beschränkungen. Nicht empfohlen für Probleme mit rangniedriger Jacobi-Matrix.
‘lm’ : Levenberg-Marquardt-Algorithmus, wie in MINPACK implementiert. Verarbeitet keine Beschränkungen und dünn besetzte Jacobi-Matrizen. Normalerweise der effizienteste Algorithmus für kleine unbeschränkte Probleme.

Standard ist 'trf'. Siehe Hinweise für weitere Informationen.

ftolfloat oder None, optional

Toleranz für die Beendigung durch die Änderung der Kostenfunktion. Standard ist 1e-8. Der Optimierungsprozess wird gestoppt, wenn dF < ftol * F und in letztem Schritt eine angemessene Übereinstimmung zwischen einem lokalen quadratischen Modell und dem wahren Modell bestand.

Wenn None und 'method' nicht 'lm' ist, wird die Beendigung durch diese Bedingung deaktiviert. Wenn 'method' 'lm' ist, muss diese Toleranz größer als die Maschinenepsilon sein.

xtolfloat oder None, optional

Toleranz für die Beendigung durch die Änderung der unabhängigen Variablen. Standard ist 1e-8. Die genaue Bedingung hängt von der verwendeten method ab

Für 'trf' und 'dogbox' : norm(dx) < xtol * (xtol + norm(x)).
Für 'lm' : Delta < xtol * norm(xs), wobei Delta der Radius einer Trust-Region und xs der Wert von x skaliert gemäß dem Parameter x_scale (siehe unten) ist.

Wenn None und 'method' nicht 'lm' ist, wird die Beendigung durch diese Bedingung deaktiviert. Wenn 'method' 'lm' ist, muss diese Toleranz größer als die Maschinenepsilon sein.

gtolfloat oder None, optional

Toleranz für die Beendigung durch die Norm des Gradienten. Standard ist 1e-8. Die genaue Bedingung hängt von der verwendeten method ab

Für 'trf' : norm(g_scaled, ord=np.inf) < gtol, wobei g_scaled der skalierte Gradient ist, der die Beschränkungen berücksichtigt [STIR].
Für 'dogbox' : norm(g_free, ord=np.inf) < gtol, wobei g_free der Gradient bezüglich der Variablen ist, die sich nicht im optimalen Zustand an der Grenze befinden.
Für 'lm' : der maximale Absolutwert des Kosinus der Winkel zwischen den Spalten der Jacobi-Matrix und dem Residuenvektor ist kleiner als gtol, oder der Residuenvektor ist Null.

Wenn None und 'method' nicht 'lm' ist, wird die Beendigung durch diese Bedingung deaktiviert. Wenn 'method' 'lm' ist, muss diese Toleranz größer als die Maschinenepsilon sein.

x_scale{None, array_like, ‘jac’}, optional

Charakteristische Skala jeder Variablen. Das Setzen von x_scale ist äquivalent zur Umformulierung des Problems in skalierten Variablen xs = x / x_scale. Eine alternative Sichtweise ist, dass die Größe einer Trust-Region entlang der j-ten Dimension proportional zu x_scale[j] ist. Verbesserte Konvergenz kann durch das Setzen von x_scale erreicht werden, so dass ein Schritt einer bestimmten Größe entlang einer der skalierten Variablen ähnliche Auswirkungen auf die Kostenfunktion hat. Wenn auf 'jac' gesetzt, wird die Skala iterativ anhand der inversen Normen der Spalten der Jacobi-Matrix aktualisiert (wie in [JJMore] beschrieben). Die Standard-Skalierung für jede Methode (d.h. wenn x_scale ist None) ist wie folgt

Für 'trf' : x_scale == 1
Für 'dogbox' : x_scale == 1
Für 'jac' : x_scale == 'jac'

Geändert in Version 1.16.0: Der Standardwert des Schlüsselworts wird von 1 auf None geändert, um anzuzeigen, dass ein Standardansatz für die Skalierung verwendet wird. Für die Methode 'lm' wird die Standard-Skalierung von 1 auf 'jac' geändert. Dies hat sich als bessere Leistung erwiesen und ist die gleiche Skalierung wie bei leastsq.

lossstr oder callable, optional

Bestimmt die Verlustfunktion. Folgende Schlüsselwörter sind erlaubt

‘linear’ (Standard) : rho(z) = z. Ergibt ein Standard-Kleinste-Quadrate-Problem.
‘soft_l1’ : rho(z) = 2 * ((1 + z)**0.5 - 1). Die glatte Approximation des L1-Verlusts (Absolutwert). Normalerweise eine gute Wahl für robuste Kleinste Quadrate.
‘huber’ : rho(z) = z if z <= 1 else 2*z**0.5 - 1. Funktioniert ähnlich wie 'soft_l1'.
‘cauchy’ : rho(z) = ln(1 + z). Schwächt den Einfluss von Ausreißern stark ab, kann aber zu Schwierigkeiten im Optimierungsprozess führen.
‘arctan’ : rho(z) = arctan(z). Begrenzt einen maximalen Verlust für ein einzelnes Residuum, hat ähnliche Eigenschaften wie 'cauchy'.

Wenn callable, muss sie ein 1D-ndarray z=f**2 aufnehmen und ein Array_like mit der Form (3, m) zurückgeben, wobei Zeile 0 die Funktionswerte, Zeile 1 die ersten Ableitungen und Zeile 2 die zweiten Ableitungen enthält. Die Methode 'lm' unterstützt nur den 'linear'-Verlust.

f_scalefloat, optional

Wert der weichen Grenze zwischen Inlier- und Outlier-Residuen, Standard ist 1.0. Die Verlustfunktion wird ausgewertet als rho_(f**2) = C**2 * rho(f**2 / C**2), wobei C f_scale ist und rho durch den Parameter loss bestimmt wird. Dieser Parameter hat keine Auswirkung bei loss='linear', ist aber bei anderen loss-Werten von entscheidender Bedeutung.

max_nfevNone oder int, optional

Für alle Methoden steuert dieser Parameter die maximale Anzahl von Funktionsauswertungen, die von jeder Methode verwendet werden, getrennt von denen, die zur numerischen Approximation des Jakobi verwendet werden. Wenn None (Standard), wird der Wert automatisch als 100 * n gewählt.

Geändert in Version 1.16.0: Der Standardwert für die Methode 'lm' wird auf 100 * n geändert, sowohl für eine callable als auch für eine numerisch geschätzte Jacobi-Matrix. Zuvor war der Standardwert bei Verwendung einer geschätzten Jacobi-Matrix 100 * n * (n + 1), da die Methode die zur Schätzung verwendeten Auswertungen einschloss.

diff_stepNone oder array_like, optional

Bestimmt die relative Schrittgröße für die endliche Differenz-Approximation des Jakobi. Der tatsächliche Schritt wird als x * diff_step berechnet. Wenn None (Standard), dann wird diff_step als konventionelle "optimale" Potenz der Maschinenepsilon für das verwendete Differenzenverfahren genommen [NR].

tr_solver{None, ‘exact’, ‘lsmr’}, optional

Methode zur Lösung von Trust-Region-Subproblemen, relevant nur für die Methoden 'trf' und 'dogbox'.

‘exact’ ist geeignet für nicht sehr große Probleme mit dichten Jacobi-Matrizen. Die Rechenkomplexität pro Iteration ist vergleichbar mit einer Singulärwertzerlegung der Jacobi-Matrix.
‘lsmr’ ist geeignet für Probleme mit dünn besetzten und großen Jacobi-Matrizen. Sie verwendet das iterative Verfahren scipy.sparse.linalg.lsmr zur Lösung eines linearen Kleinste-Quadrate-Problems und erfordert nur Matrix-Vektor-Produkt-Auswertungen.

Wenn None (Standard), wird der Solver basierend auf dem Typ der in der ersten Iteration zurückgegebenen Jacobi-Matrix gewählt.

tr_optionsdict, optional

Schlüsselwortoptionen, die an den Trust-Region-Solver übergeben werden.

tr_solver='exact': tr_options werden ignoriert.
tr_solver='lsmr': Optionen für scipy.sparse.linalg.lsmr. Zusätzlich unterstützt method='trf' die Option 'regularize' (bool, Standard ist True), die einen Regularisierungsterm zur Normalengleichung hinzufügt, was die Konvergenz verbessert, wenn die Jacobi-Matrix rangniedrig ist [Byrd] (Gleichung 3.4).

jac_sparsity{None, array_like, sparse array}, optional

Definiert die Sparsity-Struktur der Jacobi-Matrix für die endliche Differenz-Schätzung, ihre Form muss (m, n) sein. Wenn die Jacobi-Matrix in jeder Zeile nur wenige Nicht-Null-Elemente hat, beschleunigt die Angabe der Sparsity-Struktur die Berechnungen erheblich [Curtis]. Ein Null-Eintrag bedeutet, dass ein entsprechendes Element in der Jacobi-Matrix identisch Null ist. Wenn angegeben, wird die Verwendung des 'lsmr'-Trust-Region-Solvers erzwungen. Wenn None (Standard), wird eine dichte Differenzierung verwendet. Hat keine Auswirkung auf die Methode 'lm'.

verbose{0, 1, 2}, optional

Level der Ausführlichkeit des Algorithmus

0 (Standard) : arbeitet leise.
1 : zeigt einen Beendigungsbericht an.
2 : zeigt den Fortschritt während der Iterationen an (nicht unterstützt von der Methode 'lm').

args, kwargstuple und dict, optional

Zusätzliche Argumente, die an fun und jac übergeben werden. Beide sind standardmäßig leer. Die Aufrufsignatur ist fun(x, *args, **kwargs) und dieselbe für jac.

callbackNone oder callable, optional

Callback-Funktion, die vom Algorithmus bei jeder Iteration aufgerufen wird. Diese kann verwendet werden, um die Optimierungsergebnisse bei jedem Schritt anzuzeigen oder zu plotten und den Optimierungsalgorithmus basierend auf einer benutzerdefinierten Bedingung zu stoppen. Nur implementiert für die Methoden trf und dogbox.

Die Signatur ist callback(intermediate_result: OptimizeResult)

intermediate_result ist ein `scipy.optimize.OptimizeResult` das die Zwischenergebnisse der Optimierung bei der aktuellen Iteration enthält.

Der Callback unterstützt auch eine Signatur wie: callback(x)

Introspektion wird verwendet, um festzustellen, welche der Signaturen aufgerufen wird.

Wenn die callback-Funktion StopIteration auslöst, stoppt der Optimierungsalgorithmus und gibt den Statuscode -2 zurück.

Hinzugefügt in Version 1.16.0.

workersmap-ähnliches callable, optional
Ein map-ähnlicher aufrufbarer Typ, wie z.B. multiprocessing.Pool.map, zur parallelen Auswertung von numerischen Differenzierungen. Diese Auswertung erfolgt als workers(fun, iterable).

Hinzugefügt in Version 1.16.0.

Rückgabe:

resultOptimizeResult
OptimizeResult mit den folgenden definierten Feldern

xndarray, Form (n,)
Gefundene Lösung.

costfloat
Wert der Kostenfunktion an der Lösung.

funndarray, Form (m,)
Vektor der Residuen an der Lösung.

jacndarray, Sparse Array oder LinearOperator, Form (m, n)
Modifizierte Jacobi-Matrix an der Lösung, in dem Sinne, dass J^T J eine Gauss-Newton-Näherung der Hesse-Matrix der Kostenfunktion ist. Der Typ ist derselbe wie der vom Algorithmus verwendete.

gradndarray, Form (m,)
Gradient der Kostenfunktion an der Lösung.

optimalityfloat
Maß für die Optimalität erster Ordnung. Bei unbeschränkten Problemen ist dies immer die uniforme Norm des Gradienten. Bei beschränkten Problemen ist dies die Größe, die während der Iterationen mit gtol verglichen wurde.

active_maskndarray von int, Form (n,)
Jede Komponente zeigt an, ob eine entsprechende Beschränkung aktiv ist (d.h. ob eine Variable an der Grenze liegt)

0 : eine Beschränkung ist nicht aktiv.

-1 : eine untere Grenze ist aktiv.

1 : eine obere Grenze ist aktiv.

Kann für die Methode 'trf' etwas willkürlich sein, da sie eine Folge von streng zulässigen Iterationen erzeugt und active_mask innerhalb eines Toleranzschwellenwerts bestimmt wird.

nfevint
Anzahl der durchgeführten Funktionsauswertungen. Diese Zahl enthält nicht die Funktionsaufrufe zur numerischen Jacobi-Approximation.

Geändert in Version 1.16.0: Für die Methode 'lm' werden die zur numerischen Jacobi-Approximation verwendeten Funktionsaufrufe nicht mehr gezählt. Dies dient der Angleichung aller Methoden.

njevint oder None
Anzahl der durchgeführten Jacobi-Auswertungen. Wenn im 'lm'-Verfahren eine numerische Jacobi-Approximation verwendet wird, wird dieser Wert auf None gesetzt.

statusint
Der Grund für die Beendigung des Algorithmus

-2 : Beendet, weil der Callback StopIteration ausgelöst hat.

-1 : Unkorrekte Eingabeparameter, Status von MINPACK zurückgegeben.

0 : Die maximale Anzahl von Funktionsauswertungen wurde überschritten.

1 : Die Abbruchbedingung gtol ist erfüllt.

2 : Die Abbruchbedingung ftol ist erfüllt.

3 : Die Abbruchbedingung xtol ist erfüllt.

4 : Sowohl die Bedingungen ftol als auch xtol sind erfüllt.

messagestr
Verbale Beschreibung des Abbruchgrundes.

successbool
True, wenn eine der Konvergenzkriterien erfüllt ist (status > 0).

Siehe auch

leastsq
Ein älterer Wrapper für die MINPACK-Implementierung des Levenberg-Marquardt-Algorithmus.

curve_fit
Kleinste-Quadrate-Minimierung angewendet auf ein Kurvenanpassungsproblem.

Hinweise

Die Methode 'lm' (Levenberg-Marquardt) ruft einen Wrapper für einen in MINPACK implementierten Kleinste-Quadrate-Algorithmus auf (lmder). Sie führt den Levenberg-Marquardt-Algorithmus aus, der als Trust-Region-Algorithmus formuliert ist. Die Implementierung basiert auf dem Artikel [JJMore], ist sehr robust und effizient mit vielen cleveren Tricks. Sie sollte Ihre erste Wahl für unbeschränkte Probleme sein. Beachten Sie, dass sie keine Beschränkungen unterstützt. Außerdem funktioniert sie nicht, wenn m < n.

Die Methode 'trf' (Trust Region Reflective) ist motiviert durch den Prozess der Lösung eines Gleichungssystems, das die Optimierungsbedingung erster Ordnung für ein beschränktes Minimierungsproblem darstellt, wie in [STIR] formuliert. Der Algorithmus löst iterativ Trust-Region-Subprobleme, die um einen speziellen quadratischen Diagonalterm erweitert und mit einer Trust-Region-Form, die durch den Abstand zu den Grenzen und die Richtung des Gradienten bestimmt wird, versehen sind. Diese Verbesserungen helfen, Schritte direkt in die Grenzen hinein zu vermeiden und den gesamten Variablenraum effizient zu erkunden. Um theoretische Anforderungen zu erfüllen, hält der Algorithmus die Iterierten strikt zulässig. Bei dichten Jacobi-Matrizen werden die Trust-Region-Subprobleme mit einer exakten Methode gelöst, die der in [JJMore] beschriebenen (und in MINPACK implementierten) sehr ähnlich ist. Der Unterschied zur MINPACK-Implementierung besteht darin, dass pro Iteration eine Singulärwertzerlegung der Jacobi-Matrix durchgeführt wird, anstelle einer QR-Zerlegung und einer Reihe von Givens-Rotationen. Für große dünn besetzte Jacobi-Matrizen wird ein 2D-Unterraumansatz zum Lösen von Trust-Region-Subproblemen verwendet [STIR], [Byrd]. Der Unterraum wird von einem skalierten Gradienten und einer approximierten Gauss-Newton-Lösung, die von scipy.sparse.linalg.lsmr geliefert wird, aufgespannt. Wenn keine Beschränkungen auferlegt werden, ähnelt der Algorithmus stark MINPACK und hat eine vergleichbare Leistung. Der Algorithmus ist bei unbeschränkten und beschränkten Problemen recht robust, daher ist er der Standardalgorithmus.

Die Methode 'dogbox' arbeitet im Trust-Region-Framework, verwendet jedoch rechteckige Trust-Regionen im Gegensatz zu konventionellen Ellipsen [Voglis]. Der Schnittpunkt einer aktuellen Trust-Region und anfänglicher Grenzen ist wieder rechteckig, so dass auf jeder Iteration ein quadratisches Minimierungsproblem mit Grenzbedingungen annähernd mit Powells Dogleg-Methode gelöst wird [NumOpt]. Der erforderliche Gauss-Newton-Schritt kann für dichte Jacobi-Matrizen exakt oder für große dünn besetzte Jacobi-Matrizen approximativ durch scipy.sparse.linalg.lsmr berechnet werden. Der Algorithmus zeigt wahrscheinlich eine langsame Konvergenz, wenn der Rang der Jacobi-Matrix kleiner ist als die Anzahl der Variablen. Der Algorithmus übertrifft 'trf' oft bei beschränkten Problemen mit einer kleinen Anzahl von Variablen.

Robuste Verlustfunktionen sind wie in [BA] beschrieben implementiert. Die Idee ist, den Residuenvektor und die Jacobi-Matrix bei jeder Iteration so zu modifizieren, dass der berechnete Gradient und die Gauss-Newton-Hesse-Näherung dem wahren Gradienten und der wahren Hesse-Näherung der Kostenfunktion entsprechen. Dann schreitet der Algorithmus normal fort, d.h. robuste Verlustfunktionen werden als einfacher Wrapper über Standard-Kleinste-Quadrate-Algorithmen implementiert.

Hinzugefügt in Version 0.17.0.

Referenzen

[STIR] (1,2,3)
M. A. Branch, T. F. Coleman, und Y. Li, „A Subspace, Interior, and Conjugate Gradient Method for Large-Scale Bound-Constrained Minimization Problems,“ SIAM Journal on Scientific Computing, Bd. 21, Nr. 1, S. 1-23, 1999.

[NR]
William H. Press et. al., „Numerical Recipes. The Art of Scientific Computing. 3. Auflage“, Abschnitt 5.7.

[Byrd] (1,2)
R. H. Byrd, R. B. Schnabel und G. A. Shultz, „Approximate solution of the trust region problem by minimization over two-dimensional subspaces“, Math. Programming, 40, S. 247-263, 1988.

[Curtis]
A. Curtis, M. J. D. Powell und J. Reid, „On the estimation of sparse Jacobian matrices“, Journal of the Institute of Mathematics and its Applications, 13, S. 117-120, 1974.

[JJMore] (1,2,3)
J. J. More, „The Levenberg-Marquardt Algorithm: Implementation and Theory,“ Numerical Analysis, hrsg. G. A. Watson, Lecture Notes in Mathematics 630, Springer Verlag, S. 105-116, 1977.

[Voglis]
C. Voglis und I. E. Lagaris, „A Rectangular Trust Region Dogleg Approach for Unconstrained and Bound Constrained Nonlinear Optimization“, WSEAS International Conference on Applied Mathematics, Korfu, Griechenland, 2004.

[NumOpt]
J. Nocedal und S. J. Wright, „Numerical optimization, 2. Auflage“, Kapitel 4.

[BA]
B. Triggs et. al., „Bundle Adjustment - A Modern Synthesis“, Proceedings of the International Workshop on Vision Algorithms: Theory and Practice, S. 298-372, 1999.

Beispiele

In diesem Beispiel finden wir ein Minimum der Rosenbrock-Funktion ohne Beschränkungen für die unabhängigen Variablen.

>>> import numpy as np >>> def fun_rosenbrock(x): ... return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])

Beachten Sie, dass wir nur den Vektor der Residuen angeben. Der Algorithmus konstruiert die Kostenfunktion als Summe der Quadrate der Residuen, was die Rosenbrock-Funktion ergibt. Das exakte Minimum liegt bei x = [1.0, 1.0].

>>> from scipy.optimize import least_squares >>> x0_rosenbrock = np.array([2, 2]) >>> res_1 = least_squares(fun_rosenbrock, x0_rosenbrock) >>> res_1.x array([ 1., 1.]) >>> res_1.cost 9.8669242910846867e-30 >>> res_1.optimality 8.8928864934219529e-14

Wir beschränken nun die Variablen so, dass die vorherige Lösung unzulässig wird. Insbesondere fordern wir, dass x[1] >= 1.5 ist und x[0] unbeschränkt bleibt. Zu diesem Zweck geben wir den Parameter bounds für least_squares in der Form bounds=([-np.inf, 1.5], np.inf) an.

Wir geben auch die analytische Jacobi-Matrix an

>>> def jac_rosenbrock(x): ... return np.array([ ... [-20 * x[0], 10], ... [-1, 0]])

Wenn wir dies alles zusammenfassen, sehen wir, dass die neue Lösung an der Grenze liegt

>>> res_2 = least_squares(fun_rosenbrock, x0_rosenbrock, jac_rosenbrock, ... bounds=([-np.inf, 1.5], np.inf)) >>> res_2.x array([ 1.22437075, 1.5 ]) >>> res_2.cost 0.025213093946805685 >>> res_2.optimality 1.5885401433157753e-07

Nun lösen wir ein Gleichungssystem (d.h. die Kostenfunktion sollte an einem Minimum Null sein) für eine Broyden tridiagonale vektorwertige Funktion mit 100000 Variablen

>>> def fun_broyden(x): ... f = (3 - x) * x + 1 ... f[1:] -= x[:-1] ... f[:-1] -= 2 * x[1:] ... return f

Die entsprechende Jacobi-Matrix ist dünn besetzt. Wir weisen den Algorithmus an, sie durch endliche Differenzen zu schätzen, und geben die Sparsity-Struktur der Jacobi-Matrix an, um diesen Prozess erheblich zu beschleunigen.

>>> from scipy.sparse import lil_array >>> def sparsity_broyden(n): ... sparsity = lil_array((n, n), dtype=int) ... i = np.arange(n) ... sparsity[i, i] = 1 ... i = np.arange(1, n) ... sparsity[i, i - 1] = 1 ... i = np.arange(n - 1) ... sparsity[i, i + 1] = 1 ... return sparsity ... >>> n = 100000 >>> x0_broyden = -np.ones(n) ... >>> res_3 = least_squares(fun_broyden, x0_broyden, ... jac_sparsity=sparsity_broyden(n)) >>> res_3.cost 4.5687069299604613e-23 >>> res_3.optimality 1.1650454296851518e-11

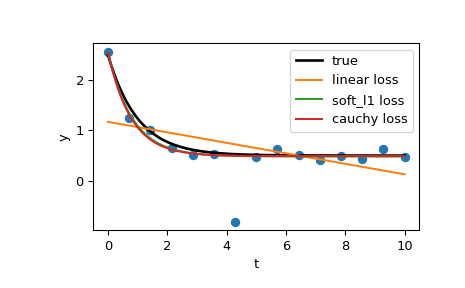
Betrachten wir nun ein Kurvenanpassungsproblem mit einer robusten Verlustfunktion, um Ausreißer in den Daten zu berücksichtigen. Definieren wir die Modellfunktion als y = a + b * exp(c * t), wobei t eine Prädiktorvariable ist, y eine Beobachtung und a, b, c die zu schätzenden Parameter sind.

Zuerst definieren wir die Funktion, die die Daten mit Rauschen und Ausreißern generiert, definieren die Modellparameter und generieren die Daten

>>> from numpy.random import default_rng >>> rng = default_rng() >>> def gen_data(t, a, b, c, noise=0., n_outliers=0, seed=None): ... rng = default_rng(seed) ... ... y = a + b * np.exp(t * c) ... ... error = noise * rng.standard_normal(t.size) ... outliers = rng.integers(0, t.size, n_outliers) ... error[outliers] *= 10 ... ... return y + error ... >>> a = 0.5 >>> b = 2.0 >>> c = -1 >>> t_min = 0 >>> t_max = 10 >>> n_points = 15 ... >>> t_train = np.linspace(t_min, t_max, n_points) >>> y_train = gen_data(t_train, a, b, c, noise=0.1, n_outliers=3)

Definieren Sie die Funktion zur Berechnung der Residuen und die Anfangsschätzung der Parameter.

>>> def fun(x, t, y): ... return x[0] + x[1] * np.exp(x[2] * t) - y ... >>> x0 = np.array([1.0, 1.0, 0.0])

Berechnen Sie eine Standard-Kleinste-Quadrate-Lösung

>>> res_lsq = least_squares(fun, x0, args=(t_train, y_train))

Berechnen Sie nun zwei Lösungen mit zwei verschiedenen robusten Verlustfunktionen. Der Parameter f_scale ist auf 0.1 gesetzt, was bedeutet, dass Inlier-Residuen 0.1 (das verwendete Rauschlevel) nicht signifikant überschreiten sollten.

>>> res_soft_l1 = least_squares(fun, x0, loss='soft_l1', f_scale=0.1, ... args=(t_train, y_train)) >>> res_log = least_squares(fun, x0, loss='cauchy', f_scale=0.1, ... args=(t_train, y_train))

Und schließlich plottet alle Kurven. Wir sehen, dass wir durch die Auswahl eines geeigneten loss Schätzungen erhalten können, die auch bei starken Ausreißern nahe dem Optimum liegen. Beachten Sie jedoch, dass es im Allgemeinen empfohlen wird, zuerst die 'soft_l1'- oder 'huber'-Verlustfunktionen auszuprobieren (falls überhaupt notwendig), da die anderen beiden Optionen zu Schwierigkeiten im Optimierungsprozess führen können.

>>> t_test = np.linspace(t_min, t_max, n_points * 10) >>> y_true = gen_data(t_test, a, b, c) >>> y_lsq = gen_data(t_test, *res_lsq.x) >>> y_soft_l1 = gen_data(t_test, *res_soft_l1.x) >>> y_log = gen_data(t_test, *res_log.x) ... >>> import matplotlib.pyplot as plt >>> plt.plot(t_train, y_train, 'o') >>> plt.plot(t_test, y_true, 'k', linewidth=2, label='true') >>> plt.plot(t_test, y_lsq, label='linear loss') >>> plt.plot(t_test, y_soft_l1, label='soft_l1 loss') >>> plt.plot(t_test, y_log, label='cauchy loss') >>> plt.xlabel("t") >>> plt.ylabel("y") >>> plt.legend() >>> plt.show()

Im folgenden Beispiel zeigen wir, wie komplexwertige Residuenfunktionen komplexer Variablen mit least_squares() optimiert werden können. Betrachten Sie die folgende Funktion

>>> def f(z): ... return z - (0.5 + 0.5j)

Wir packen sie in eine Funktion reeller Variablen, die reelle Residuen zurückgibt, indem wir einfach die reellen und imaginären Teile als unabhängige Variablen behandeln

>>> def f_wrap(x): ... fx = f(x[0] + 1j*x[1]) ... return np.array([fx.real, fx.imag])

Somit optimieren wir anstelle der ursprünglichen m-dimensionalen komplexen Funktion von n komplexen Variablen eine 2m-dimensionale reelle Funktion von 2n reellen Variablen

>>> from scipy.optimize import least_squares >>> res_wrapped = least_squares(f_wrap, (0.1, 0.1), bounds=([0, 0], [1, 1])) >>> z = res_wrapped.x[0] + res_wrapped.x[1]*1j >>> z (0.49999999999925893+0.49999999999925893j)

vorherige

direct

nächste

nnls

Auf dieser Seite

least_squares