newton#
- scipy.optimize.newton(func, x0, fprime=None, args=(), tol=1.48e-08, maxiter=50, fprime2=None, x1=None, rtol=0.0, full_output=False, disp=True)[Quelle]#
Findet eine Nullstelle einer reellen oder komplexen Funktion mithilfe der Newton-Raphson-Methode (oder Sekanten- oder Halley-Methode).
Findet eine Nullstelle der skalarwertigen Funktion func, gegeben einen nahegelegenen skalaren Startpunkt x0. Die Newton-Raphson-Methode wird verwendet, wenn die Ableitung fprime von func bereitgestellt wird, andernfalls wird die Sekantenmethode verwendet. Wenn die zweite Ableitung fprime2 von func ebenfalls bereitgestellt wird, dann wird die Halley-Methode verwendet.
Wenn x0 eine Sequenz mit mehr als einem Element ist, gibt
newtonein Array zurück: die Nullstellen der Funktion von jedem (skalaren) Startpunkt in x0. In diesem Fall muss func vektorisiert sein, um eine Sequenz oder ein Array mit der gleichen Form wie sein erstes Argument zurückzugeben. Wenn fprime (fprime2) gegeben ist, muss dessen Rückgabe ebenfalls die gleiche Form haben: jedes Element ist die erste (zweite) Ableitung von func bezüglich seiner einzigen Variable, ausgewertet an jedem Element seines ersten Arguments.newtondient dem Finden von Nullstellen skalarwertiger Funktionen einer einzelnen Variable. Für Probleme mit mehreren Variablen sieheroot.- Parameter:
- funccallable
Die Funktion, deren Nullstelle gesucht wird. Sie muss eine Funktion einer einzelnen Variable der Form
f(x,a,b,c...)sein, wobeia,b,c...zusätzliche Argumente sind, die im Parameter args übergeben werden können.- x0float, Sequenz oder ndarray
Eine anfängliche Schätzung der Nullstelle, die sich nahe der tatsächlichen Nullstelle befinden sollte. Wenn nicht skalar, muss func vektorisiert sein und eine Sequenz oder ein Array mit der gleichen Form wie sein erstes Argument zurückgeben.
- fprimecallable, optional
Die Ableitung der Funktion, wenn verfügbar und praktisch. Wenn sie None (Standard) ist, wird die Sekantenmethode verwendet.
- argstuple, optional
Zusätzliche Argumente, die in den Funktionsaufruf einbezogen werden.
- tolfloat, optional
Der zulässige Fehler des Werts der Nullstelle. Wenn func komplexwertig ist, wird ein größerer tol empfohlen, da sowohl die reellen als auch die imaginären Teile von x zu
|x - x0|beitragen.- maxiterint, optional
Maximale Anzahl von Iterationen.
- fprime2callable, optional
Die zweite Ableitung der Funktion, wenn verfügbar und praktisch. Wenn sie None (Standard) ist, wird die normale Newton-Raphson-Methode oder die Sekantenmethode verwendet. Wenn sie nicht None ist, wird die Halley-Methode verwendet.
- x1float, optional
Eine weitere Schätzung der Nullstelle, die sich nahe der tatsächlichen Nullstelle befinden sollte. Wird verwendet, wenn fprime nicht bereitgestellt wird.
- rtolfloat, optional
Toleranz (relativ) für die Beendigung.
- full_outputbool, optional
Wenn full_output False (Standard) ist, wird die Nullstelle zurückgegeben. Wenn True und x0 skalar ist, ist der Rückgabewert
(x, r), wobeixdie Nullstelle undreinRootResults-Objekt ist. Wenn True und x0 nicht skalar ist, ist der Rückgabewert(x, converged, zero_der)(siehe Abschnitt Returns für Details).- dispbool, optional
Wenn True, wird ein RuntimeError ausgelöst, wenn der Algorithmus nicht konvergiert ist, wobei die Fehlermeldung die Anzahl der Iterationen und den aktuellen Funktionswert enthält. Andernfalls wird der Konvergenzstatus in einem
RootResults-Rückgabeobjekt aufgezeichnet. Ignoriert, wenn x0 nicht skalar ist. *Hinweis: Dies hat wenig mit der Anzeige zu tun, jedoch kann das `disp`-Schlüsselwort aus Kompatibilitätsgründen nicht umbenannt werden.*
- Rückgabe:
- rootfloat, Sequenz oder ndarray
Geschätzter Ort, an dem die Funktion Null ist.
- r
RootResults, optional Vorhanden, wenn
full_output=Trueund x0 skalar ist. Objekt, das Informationen über die Konvergenz enthält. Insbesondere istr.convergedTrue, wenn die Routine konvergiert ist.- convergedndarray von bool, optional
Vorhanden, wenn
full_output=Trueund x0 nicht skalar ist. Für Vektorfunktionen gibt an, welche Elemente erfolgreich konvergiert sind.- zero_derndarray von bool, optional
Vorhanden, wenn
full_output=Trueund x0 nicht skalar ist. Für Vektorfunktionen gibt an, welche Elemente eine Null-Ableitung hatten.
Siehe auch
root_scalarSchnittstelle zu Nullstellenlösern für skalare Funktionen
rootSchnittstelle zu Nullstellenlösern für Funktionen mit mehreren Eingängen und Ausgängen
Hinweise
Die Konvergenzrate der Newton-Raphson-Methode ist quadratisch, die Halley-Methode kubisch und die Sekantenmethode sub-quadratisch. Das bedeutet, dass, wenn die Funktion sich gut verhält, der tatsächliche Fehler in der geschätzten Nullstelle nach der n-ten Iteration ungefähr das Quadrat (Kubik für Halley) des Fehlers nach dem (n-1)-ten Schritt ist. Das hier verwendete Abbruchkriterium ist jedoch die Schrittweite und es gibt keine Garantie, dass eine Nullstelle gefunden wurde. Folglich sollte das Ergebnis überprüft werden. Sicherere Algorithmen sind brentq, brenth, ridder und bisect, aber sie erfordern alle, dass die Nullstelle zuerst in einem Intervall, in dem die Funktion das Vorzeichen wechselt, eingeklammert wird. Der brentq-Algorithmus wird für allgemeine Anwendungsfälle in eindimensionalen Problemen empfohlen, wenn ein solches Intervall gefunden wurde.
Wenn
newtonmit Arrays verwendet wird, eignet er sich am besten für die folgenden Arten von ProblemenDie Anfangsschätzungen, x0, sind alle relativ gleich weit von den Nullstellen entfernt.
Einige oder alle zusätzlichen Argumente, args, sind ebenfalls Arrays, so dass eine Klasse ähnlicher Probleme gemeinsam gelöst werden kann.
Die Größe der Anfangsschätzungen, x0, ist größer als O(100) Elemente. Andernfalls kann eine naive Schleife genauso gut oder besser performen als eine Vektorisierung.
Beispiele
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy import optimize
>>> def f(x): ... return (x**3 - 1) # only one real root at x = 1
fprimewird nicht bereitgestellt, verwende die Sekantenmethode>>> root = optimize.newton(f, 1.5) >>> root 1.0000000000000016 >>> root = optimize.newton(f, 1.5, fprime2=lambda x: 6 * x) >>> root 1.0000000000000016
Nur
fprimewird bereitgestellt, verwende die Newton-Raphson-Methode>>> root = optimize.newton(f, 1.5, fprime=lambda x: 3 * x**2) >>> root 1.0
Sowohl
fprime2als auchfprimewerden bereitgestellt, verwende die Halley-Methode>>> root = optimize.newton(f, 1.5, fprime=lambda x: 3 * x**2, ... fprime2=lambda x: 6 * x) >>> root 1.0
Wenn wir Nullstellen für eine Reihe von verwandten Startwerten und/oder Funktionsparametern finden wollen, können wir beides als Eingabearray bereitstellen
>>> f = lambda x, a: x**3 - a >>> fder = lambda x, a: 3 * x**2 >>> rng = np.random.default_rng() >>> x = rng.standard_normal(100) >>> a = np.arange(-50, 50) >>> vec_res = optimize.newton(f, x, fprime=fder, args=(a, ), maxiter=200)
Das obige ist das Äquivalent zur separaten Lösung für jeden Wert in
(x, a)in einer for-Schleife, nur schneller>>> loop_res = [optimize.newton(f, x0, fprime=fder, args=(a0,), ... maxiter=200) ... for x0, a0 in zip(x, a)] >>> np.allclose(vec_res, loop_res) True
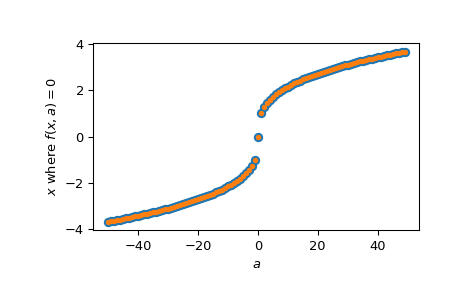
Plotten der Ergebnisse für alle Werte von
a>>> analytical_result = np.sign(a) * np.abs(a)**(1/3) >>> fig, ax = plt.subplots() >>> ax.plot(a, analytical_result, 'o') >>> ax.plot(a, vec_res, '.') >>> ax.set_xlabel('$a$') >>> ax.set_ylabel('$x$ where $f(x, a)=0$') >>> plt.show()