scipy.signal.

ZoomFFT#

class scipy.signal.ZoomFFT(n, fn, m=None, *, fs=2, endpoint=False)[Quelle]#

Erzeugt eine aufrufbare Zoom-FFT-Transformationsfunktion.

Dies ist eine Spezialisierung der Chirp Z-Transformation (CZT) für eine Menge gleichmäßig verteilter Frequenzen um den Einheitskreis, die verwendet wird, um einen Abschnitt der FFT effizienter zu berechnen, als die gesamte FFT zu berechnen und abzuschneiden.

Parameter:

nint: Die Größe des Signals.
fnarray_like: Eine Sequenz der Länge 2 [f1, f2], die den Frequenzbereich angibt, oder ein Skalar, für den der Bereich [0, fn] angenommen wird.
mint, optional: Die Anzahl der zu evaluierenden Punkte. Standard ist n.
fsfloat, optional: Die Abtastfrequenz. Wenn fs=10 beispielsweise 10 kHz repräsentierte, dann wären f1 und f2 ebenfalls in kHz angegeben. Die standardmäßige Abtastfrequenz ist 2, sodass f1 und f2 im Bereich [0, 1] liegen sollten, um die Transformation unterhalb der Nyquist-Frequenz zu halten.
endpointbool, optional: Wenn True, ist f2 die letzte Stichprobe. Andernfalls ist sie nicht enthalten. Standard ist False.

Methoden

`__call__`(x, *[, axis])	Berechnet die Chirp-Z-Transformation eines Signals.
`points`()	Gibt die Punkte zurück, an denen die Chirp-Z-Transformation berechnet wird.

Rückgabe:

fZoomFFT: Aufrufbares Objekt f(x, axis=-1) zur Berechnung der Zoom-FFT auf x.

Siehe auch

zoom_fft: Bequeme Funktion zur Berechnung einer Zoom-FFT.

Hinweise

Die Standardwerte sind so gewählt, dass f(x, 2) äquivalent zu fft.fft(x) ist und, wenn m > len(x), dass f(x, 2, m) äquivalent zu fft.fft(x, m) ist.

Die Abtastfrequenz ist 1/dt, der Zeitschritt zwischen den Abtastungen im Signal x. Der Einheitskreis entspricht Frequenzen von 0 bis zur Abtastfrequenz. Die standardmäßige Abtastfrequenz von 2 bedeutet, dass f1 und f2 Werte bis zur Nyquist-Frequenz im Bereich [0, 1) liegen. Für f1 und f2, die in Radiant ausgedrückt werden, sollte eine Abtastfrequenz von 2*pi verwendet werden.

Denken Sie daran, dass eine Zoom-FFT nur die Punkte der vorhandenen FFT interpolieren kann. Sie kann nicht helfen, zwei getrennte nahe Frequenzen aufzulösen. Die Frequenzauflösung kann nur durch Erhöhung der Erfassungszeit verbessert werden.

Diese Funktionen werden mit Bluesteins Algorithmus implementiert (wie auch scipy.fft). [2]

Referenzen

[1]

Steve Alan Shilling, „A study of the chirp z-transform and its applications“, S. 29 (1970) https://krex.k-state.edu/dspace/bitstream/handle/2097/7844/LD2668R41972S43.pdf

[2]

Leo I. Bluestein, „A linear filtering approach to the computation of the discrete Fourier transform“, Northeast Electronics Research and Engineering Meeting Record 10, 218-219 (1968).

Beispiele

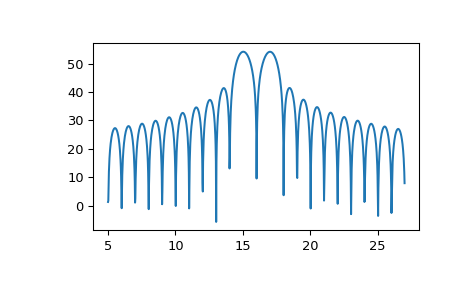
Um die Transformationsergebnisse zu plotten, verwenden Sie etwas wie das Folgende

>>> import numpy as np
>>> from scipy.signal import ZoomFFT
>>> t = np.linspace(0, 1, 1021)
>>> x = np.cos(2*np.pi*15*t) + np.sin(2*np.pi*17*t)
>>> f1, f2 = 5, 27
>>> transform = ZoomFFT(len(x), [f1, f2], len(x), fs=1021)
>>> X = transform(x)
>>> f = np.linspace(f1, f2, len(x))
>>> import matplotlib.pyplot as plt
>>> plt.plot(f, 20*np.log10(np.abs(X)))
>>> plt.show()

../../_images/scipy-signal-ZoomFFT-1.png