scipy.signal.

bilinear_zpk#

scipy.signal.bilinear_zpk(z, p, k, fs)[Quelle]#

Gibt einen digitalen IIR-Filter aus einem analogen Filter mittels einer Bilinear-Transformation zurück.

Transformiert einen Satz von Polen und Nullstellen von der analogen s-Ebene in die digitale z-Ebene unter Verwendung der Tustin-Methode, die 2*fs*(z-1) / (z+1) durch s ersetzt, wobei die Form des Frequenzgangs erhalten bleibt.

Parameter:

zarray_like: Nullstellen der Übertragungsfunktion des analogen Filters.
parray_like: Polstellen der Übertragungsfunktion des analogen Filters.
kfloat: Systemverstärkung der Übertragungsfunktion des analogen Filters.
fsfloat: Abtastrate, als normale Frequenz (z. B. Hertz). In dieser Funktion wird keine Vorkorrektur durchgeführt.

Rückgabe:

zndarray: Nullstellen der transformierten digitalen Filterübertragungsfunktion.
pndarray: Polstellen der transformierten digitalen Filterübertragungsfunktion.
kfloat: Systemverstärkung des transformierten digitalen Filters.

Siehe auch

lp2lp_zpk, lp2hp_zpk, lp2bp_zpk, lp2bs_zpk
bilinear

Hinweise

Hinzugefügt in Version 1.1.0.

Beispiele

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

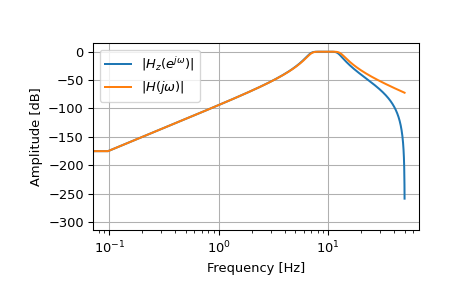
>>> fs = 100
>>> bf = 2 * np.pi * np.array([7, 13])
>>> filts = signal.lti(*signal.butter(4, bf, btype='bandpass', analog=True,
...                                   output='zpk'))
>>> filtz = signal.lti(*signal.bilinear_zpk(filts.zeros, filts.poles,
...                                         filts.gain, fs))
>>> wz, hz = signal.freqz_zpk(filtz.zeros, filtz.poles, filtz.gain)
>>> ws, hs = signal.freqs_zpk(filts.zeros, filts.poles, filts.gain,
...                           worN=fs*wz)
>>> plt.semilogx(wz*fs/(2*np.pi), 20*np.log10(np.abs(hz).clip(1e-15)),
...              label=r'$|H_z(e^{j \omega})|$')
>>> plt.semilogx(wz*fs/(2*np.pi), 20*np.log10(np.abs(hs).clip(1e-15)),
...              label=r'$|H(j \omega)|$')
>>> plt.legend()
>>> plt.xlabel('Frequency [Hz]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.grid(True)

../../_images/scipy-signal-bilinear_zpk-1.png