scipy.signal.

detrend

scipy.signal.detrend(data, axis=-1, type='linear', bp=0, overwrite_data=False)

Entfernt einen linearen oder konstanten Trend entlang einer Achse aus den Daten.

Parameter:

dataarray_like

Die Eingabedaten.

axisint, optional

Die Achse, entlang der die Daten enttrendet werden sollen. Standardmäßig ist dies die letzte Achse (-1).

type{‘linear’, ‘constant’}, optional

Der Typ des Enttrendens. Wenn type == 'linear' (Standard), wird das Ergebnis einer linearen Kleinste-Quadrate-Anpassung an data von data subtrahiert. Wenn type == 'constant', wird nur der Mittelwert von data subtrahiert.

bparray_like of ints, optional

Eine Sequenz von Bruchpunkten. Wenn angegeben, wird für jeden Teil von data zwischen zwei Bruchpunkten eine individuelle lineare Anpassung durchgeführt. Bruchpunkte werden als Indizes in data angegeben. Dieser Parameter hat nur eine Auswirkung, wenn type == 'linear'.

overwrite_databool, optional

Wenn True, wird das Enttrenden inplace durchgeführt und eine Kopie vermieden. Standard ist False.

Rückgabe:

retndarray

Die enttrendeten Eingabedaten.

Siehe auch

numpy.polynomial.polynomial.Polynomial.fit

Erstellt eine Polynomanpassung nach der Methode der kleinsten Quadrate.

Hinweise

Das Enttrenden kann als Subtraktion einer Kleinste-Quadrate-Polynomanpassung interpretiert werden: Die Einstellung des Parameters type auf 'constant' entspricht der Anpassung eines Polynoms vom Grad Null, 'linear' einem Polynom vom Grad Eins. Siehe das Beispiel unten.

Beispiele

Probieren Sie es in Ihrem Browser aus!

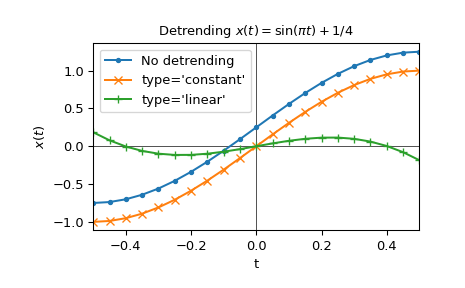
Das folgende Beispiel enttrendet die Funktion \(x(t) = \sin(\pi t) + 1/4\)

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal import detrend
...
>>> t = np.linspace(-0.5, 0.5, 21)
>>> x = np.sin(np.pi*t) + 1/4
...
>>> x_d_const = detrend(x, type='constant')
>>> x_d_linear = detrend(x, type='linear')
...
>>> fig1, ax1 = plt.subplots()
>>> ax1.set_title(r"Detrending $x(t)=\sin(\pi t) + 1/4$")
>>> ax1.set(xlabel="t", ylabel="$x(t)$", xlim=(t[0], t[-1]))
>>> ax1.axhline(y=0, color='black', linewidth=.5)
>>> ax1.axvline(x=0, color='black', linewidth=.5)
>>> ax1.plot(t, x, 'C0.-',  label="No detrending")
>>> ax1.plot(t, x_d_const, 'C1x-', label="type='constant'")
>>> ax1.plot(t, x_d_linear, 'C2+-', label="type='linear'")
>>> ax1.legend()
>>> plt.show()

Alternativ kann auch das Polynomial von NumPy zum Enttrenden verwendet werden.

>>> pp0 = np.polynomial.Polynomial.fit(t, x, deg=0)  # fit degree 0 polynomial
>>> np.allclose(x_d_const, x - pp0(t))  # compare with constant detrend
True
>>> pp1 = np.polynomial.Polynomial.fit(t, x, deg=1)  # fit degree 1 polynomial
>>> np.allclose(x_d_linear, x - pp1(t))  # compare with linear detrend
True

Beachten Sie, dass Polynomial auch die Anpassung von Polynomen höheren Grades ermöglicht. Konsultieren Sie dessen Dokumentation, wie die Polynomkoeffizienten extrahiert werden können.

ZurückIn Tab öffnen