freqs#
- scipy.signal.freqs(b, a, worN=200, plot=None)[Quelle]#
Frequenzgang eines analogen Filters berechnen.
Gegeben den Zähler b vom Grad M und den Nenner a vom Grad N eines analogen Filters, berechnen Sie dessen Frequenzgang
b[0]*(jw)**M + b[1]*(jw)**(M-1) + ... + b[M] H(w) = ---------------------------------------------- a[0]*(jw)**N + a[1]*(jw)**(N-1) + ... + a[N]
- Parameter:
- barray_like
Zähler eines linearen Filters.
- aarray_like
Nenner eines linearen Filters.
- worN{None, int, array_like}, optional
Wenn None, dann berechnen Sie bei 200 Frequenzen rund um die interessanten Teile der Antwortkurve (bestimmt durch Pol-Null-Positionen). Wenn eine einzelne Ganzzahl, dann berechnen Sie bei dieser Anzahl von Frequenzen. Andernfalls berechnen Sie die Antwort bei den Winkel-Frequenzen (z. B. rad/s), die in worN angegeben sind.
- plotcallable, optional
Ein Callable, das zwei Argumente annimmt. Wenn angegeben, werden die Rückgabeparameter w und h an plot übergeben. Nützlich zum Plotten des Frequenzgangs innerhalb von
freqs.
- Rückgabe:
- wndarray
Die Winkel-Frequenzen, bei denen h berechnet wurde.
- hndarray
Der Frequenzgang.
Siehe auch
freqzBerechnet die Frequenzantwort eines digitalen Filters.
Hinweise
Die Verwendung der "plot"-Funktion von Matplotlib als Callable für plot führt zu unerwarteten Ergebnissen; dies plottet den Realteil der komplexen Übertragungsfunktion, nicht die Magnitude. Versuchen Sie
lambda w, h: plot(w, abs(h)).Beispiele
>>> from scipy.signal import freqs, iirfilter >>> import numpy as np
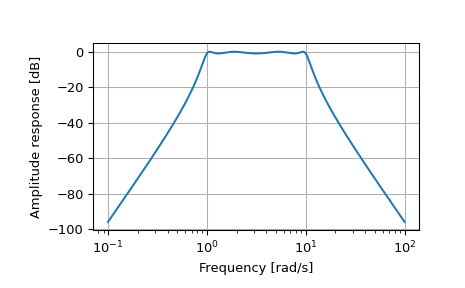
>>> b, a = iirfilter(4, [1, 10], 1, 60, analog=True, ftype='cheby1')
>>> w, h = freqs(b, a, worN=np.logspace(-1, 2, 1000))
>>> import matplotlib.pyplot as plt >>> plt.semilogx(w, 20 * np.log10(abs(h))) >>> plt.xlabel('Frequency [rad/s]') >>> plt.ylabel('Amplitude response [dB]') >>> plt.grid(True) >>> plt.show()