scipy.signal.

istft

scipy.signal.istft(Zxx, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, input_onesided=True, boundary=True, time_axis=-1, freq_axis=-2, scaling='spectrum')

Führt die inverse Kurzzeit-Fourier-Transformation (Legacy-Funktion) durch.

Veraltet

Diese Funktion gilt als Legacy und wird keine Updates mehr erhalten. Obwohl wir derzeit keine Pläne haben, sie zu entfernen, empfehlen wir, dass neuer Code modernere Alternativen verwendet. ShortTimeFFT ist eine neuere STFT / ISTFT-Implementierung mit mehr Funktionen. Ein Vergleich zwischen den Implementierungen finden Sie im Abschnitt Short-Time Fourier Transform des SciPy User Guide.

Parameter:

Zxxarray_like

STFT des zu rekonstruierenden Signals. Wenn ein rein reelles Array übergeben wird, wird es in einen komplexen Datentyp umgewandelt.

fsfloat, optional

Abtastfrequenz der Zeitreihe. Standardmäßig 1,0.

windowstr oder Tupel oder Array_like, optional

Gewünschtes Fenster zur Verwendung. Wenn window ein String oder ein Tupel ist, wird es an get_window übergeben, um die Fensterwerte zu generieren, die standardmäßig DFT-symmetrisch sind. Siehe get_window für eine Liste von Fenstern und erforderlichen Parametern. Wenn window array_like ist, wird es direkt als Fenster verwendet und seine Länge muss nperseg sein. Standardmäßig ein Hann-Fenster. Muss mit dem für die STFT-Generierung verwendeten Fenster übereinstimmen, um eine getreue Inversion zu ermöglichen.

npersegint, optional

Anzahl der Datenpunkte, die jedem STFT-Segment entsprechen. Dieser Parameter muss angegeben werden, wenn die Anzahl der Datenpunkte pro Segment ungerade ist oder wenn die STFT über nfft > nperseg aufgefüllt wurde. Wenn None, hängt der Wert von der Form von Zxx und input_onesided ab. Wenn input_onesided True ist, dann nperseg=2*(Zxx.shape[freq_axis] - 1). Andernfalls nperseg=Zxx.shape[freq_axis]. Standardmäßig None.

noverlapint, optional

Anzahl der Punkte, die zwischen den Segmenten überlappen. Wenn None, die Hälfte der Segmentlänge. Standardmäßig None. Wenn angegeben, muss die COLA-Bedingung erfüllt sein (siehe Hinweise unten) und mit dem für die STFT-Generierung verwendeten Parameter übereinstimmen. Standardmäßig None.

nfftint, optional

Anzahl der FFT-Punkte, die jedem STFT-Segment entsprechen. Dieser Parameter muss angegeben werden, wenn die STFT über nfft > nperseg aufgefüllt wurde. Wenn None, sind die Standardwerte dieselben wie für nperseg, wie oben beschrieben, mit einer Ausnahme: wenn input_onesided True ist und nperseg==2*Zxx.shape[freq_axis] - 1, nimmt nfft ebenfalls diesen Wert an. Dieser Fall ermöglicht die korrekte Inversion einer ungeraden, nicht aufgefüllten STFT mit nfft=None. Standardmäßig None.

input_onesidedbool, optional

Wenn True, interpretieren Sie das Eingabearray als einseitige FFTs, wie sie von stft mit return_onesided=True und numpy.fft.rfft zurückgegeben werden. Wenn False, interpretieren Sie die Eingabe als zweiseitige FFT. Standardmäßig True.

boundarybool, optional

Gibt an, ob das Eingangssignal an seinen Grenzen erweitert wurde, indem ein nicht-None boundary-Argument an stft übergeben wurde. Standardmäßig True.

time_axisint, optional

Wo sich die Zeitschnitte der STFT befinden; der Standard ist die letzte Achse (d.h. axis=-1).

freq_axisint, optional

Wo sich die Frequenzachse der STFT befindet; der Standard ist die vorletzte Achse (d.h. axis=-2).

scaling: {‘spectrum’, ‘psd’}

Die Standardskalierung 'spectrum' ermöglicht es, jede Frequenzlinie von Zxx als Magnitudenspektrum zu interpretieren. Die Option 'psd' skaliert jede Linie auf eine Leistungsdichtespektrum (PSD) – sie ermöglicht die Berechnung der Energie des Signals durch numerische Integration über abs(Zxx)**2.

Rückgabe:

tndarray

Array der Ausgabezeitpunkte.

xndarray

iSTFT von Zxx.

Siehe auch

stft

Kurzzeit-Fourier-Transformation

ShortTimeFFT

Neuere STFT/ISTFT-Implementierung, die mehr Funktionen bietet.

check_COLA

Prüft, ob die Constant OverLap Add (COLA) Bedingung erfüllt ist.

check_NOLA

Prüft, ob die Nicht-Null-Überlappungs-Additions- (NOLA) Bedingung erfüllt ist

Hinweise

Um die Inversion einer STFT über die inverse STFT mit istft zu ermöglichen, muss die Signalwindowing der Bedingung „nonzero overlap add“ (NOLA) gehorchen

\[\sum_{t}w^{2}[n-tH] \ne 0\]

Dies stellt sicher, dass die Normalisierungsfaktoren, die im Nenner der Gleichung für die Wiederherstellung mittels Overlap-Add auftreten

\[x[n]=\frac{\sum_{t}x_{t}[n]w[n-tH]}{\sum_{t}w^{2}[n-tH]}\]

nicht Null sind. Die NOLA-Bedingung kann mit der Funktion check_NOLA überprüft werden.

Eine STFT, die modifiziert wurde (durch Maskierung oder anderweitig), entspricht nicht zwangsläufig einem exakt realisierbaren Signal. Diese Funktion implementiert die iSTFT über den Algorithmus zur Schätzung nach kleinsten Quadraten, der in [2] beschrieben ist, welcher ein Signal erzeugt, das den mittleren quadratischen Fehler zwischen der STFT des zurückgegebenen Signals und der modifizierten STFT minimiert.

Hinzugefügt in Version 0.19.0.

Referenzen

[1]

Oppenheim, Alan V., Ronald W. Schafer, John R. Buck „Discrete-Time Signal Processing“, Prentice Hall, 1999.

[2]

Daniel W. Griffin, Jae S. Lim „Signal Estimation from Modified Short-Time Fourier Transform“, IEEE 1984, 10.1109/TASSP.1984.1164317

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

Erzeuge ein Testsignal, eine 2 Vrms Sinuswelle bei 50Hz, verrauscht mit 0,001 V**2/Hz weißem Rauschen, abgetastet bei 1024 Hz.

>>> fs = 1024
>>> N = 10*fs
>>> nperseg = 512
>>> amp = 2 * np.sqrt(2)
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / float(fs)
>>> carrier = amp * np.sin(2*np.pi*50*time)
>>> noise = rng.normal(scale=np.sqrt(noise_power),
...                    size=time.shape)
>>> x = carrier + noise

Berechne die STFT und plote ihre Magnitude

>>> f, t, Zxx = signal.stft(x, fs=fs, nperseg=nperseg)
>>> plt.figure()
>>> plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp, shading='gouraud')
>>> plt.ylim([f[1], f[-1]])
>>> plt.title('STFT Magnitude')
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.yscale('log')
>>> plt.show()

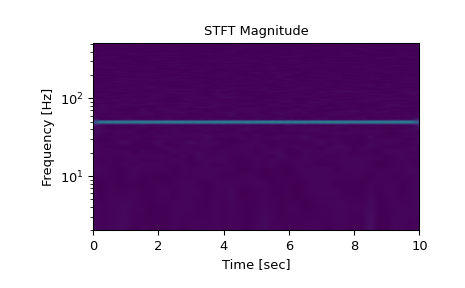
Setze die Komponenten, die 10% oder weniger der Trägermagnitude betragen, auf Null und konvertiere dann über die inverse STFT zurück in eine Zeitreihe

>>> Zxx = np.where(np.abs(Zxx) >= amp/10, Zxx, 0)
>>> _, xrec = signal.istft(Zxx, fs)

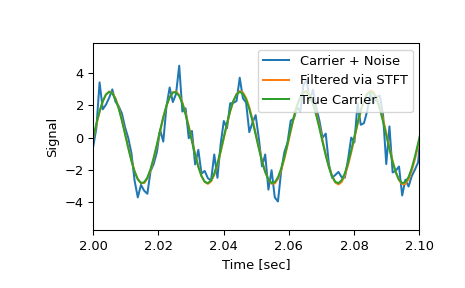
Vergleiche das bereinigte Signal mit dem Originalsignal und dem tatsächlichen Trägersignal.

>>> plt.figure()
>>> plt.plot(time, x, time, xrec, time, carrier)
>>> plt.xlim([2, 2.1])
>>> plt.xlabel('Time [sec]')
>>> plt.ylabel('Signal')
>>> plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier'])
>>> plt.show()

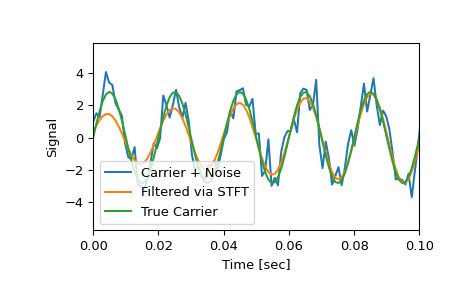
Beachten Sie, dass das bereinigte Signal nicht so abrupt beginnt wie das Original, da auch einige Koeffizienten des Transienten entfernt wurden.

>>> plt.figure()
>>> plt.plot(time, x, time, xrec, time, carrier)
>>> plt.xlim([0, 0.1])
>>> plt.xlabel('Time [sec]')
>>> plt.ylabel('Signal')
>>> plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier'])
>>> plt.show()

ZurückIn Tab öffnen