scipy.signal.

lombscargle#

scipy.signal.lombscargle(x, y, freqs, precenter=False, normalize=False, *, weights=None, floating_mean=False)[Quelle]#

Berechnet das verallgemeinerte Lomb-Scargle-Periodogramm.

Das Lomb-Scargle-Periodogramm wurde von Lomb [1] entwickelt und von Scargle [2] erweitert, um schwache periodische Signale mit ungleichmäßiger zeitlicher Abtastung zu finden und ihre Signifikanz zu testen. Der hier verwendete Algorithmus basiert auf einer gewichteten Kleinste-Quadrate-Anpassung der Form y(ω) = a*cos(ω*x) + b*sin(ω*x) + c, wobei die Anpassung für jede Frequenz unabhängig berechnet wird. Dieser Algorithmus wurde von Zechmeister und Kürster entwickelt und verbessert das Lomb-Scargle-Periodogramm, indem er die Gewichtung einzelner Abtastpunkte ermöglicht und einen unbekannten y-Offset (auch "Floating-Mean" genannt) berechnet [3]. Weitere Details und praktische Überlegungen finden Sie in der hervorragenden Referenz zum Lomb-Scargle-Periodogramm [4].

Wenn normalize False (oder "power") (Standard) ist, ist das berechnete Periodogramm unnormalisiert und nimmt für ein harmonisches Signal mit Amplitude A bei ausreichend großem N den Wert (A**2) * N/4 an. N ist die Länge von x oder y.

Wenn normalize True (oder "normalize") ist, wird das berechnete Periodogramm durch die Residuen der Daten um ein konstantes Referenzmodell (bei Null) normalisiert.

Wenn normalize "amplitude" ist, ist das berechnete Periodogramm die komplexe Darstellung von Amplitude und Phase.

Die Eingabearrays sollten eindimensional und von einem reellen Fließkommadatentyp sein, die vor der Verarbeitung in Float64-Arrays konvertiert werden.

Parameter:

xarray_like: Abtastzeiten.
yarray_like: Messwerte. Es wird angenommen, dass die Werte eine Basislinie von y = 0 haben. Wenn die Möglichkeit eines y-Offsets besteht, wird empfohlen, floating_mean auf True zu setzen.
freqsarray_like: Winkelfrequenzen (z. B. mit der Einheit rad/s=2π/s für x mit der Einheit s) für die Ausgabe des Periodogramms. Frequenzen sind normalerweise >= 0, da jeder Peak bei -freq auch bei +freq existiert.
precenterbool, optional: Zentriert die Messwerte vorab durch Subtraktion des Mittelwerts, wenn True. Dies ist ein Legacy-Parameter und unnötig, wenn floating_mean True ist.
normalizebool | str, optional: Berechnet ein normalisiertes oder komplexes (Amplitude + Phase) Periodogramm. Gültige Optionen sind: False/"power", True/"normalize" oder "amplitude".
weightsarray_like, optional: Gewichte für jede Abtastung. Gewichte müssen nicht negativ sein.
floating_meanbool, optional: Bestimmt einen y-Offset für jede Frequenz unabhängig, wenn True. Andernfalls wird angenommen, dass der y-Offset 0 ist.

Rückgabe:

pgramarray_like: Lomb-Scargle-Periodogramm.

Löst aus:

ValueError: Wenn eines der Eingabearrays x, y, freqs oder weights nicht 1D ist oder wenn eines davon eine Länge von Null hat. Oder wenn die Eingabearrays x, y und weights nicht die gleiche Form haben.
ValueError: Wenn ein Gewicht kleiner als 0 ist oder die Summe der Gewichte kleiner oder gleich 0 ist.
ValueError: Wenn der Parameter normalize nicht zu den erlaubten Optionen gehört.

Siehe auch

periodogram: Leistungsdichtespektrum mit einem Periodogramm
welch: Leistungsdichtespektrum mit Welchs Methode
csd: Kreuzleistungsdichtespektrum mit Welchs Methode

Hinweise

Der verwendete Algorithmus berücksichtigt nicht automatisch einen unbekannten y-Offset, es sei denn, floating_mean ist True. Daher wird für die meisten Anwendungsfälle empfohlen, floating_mean auf True zu setzen, wenn ein y-Offset möglich ist. Wenn precenter True ist, führt es die Operation y -= y.mean() aus. precenter ist jedoch ein Legacy-Parameter und unnötig, wenn floating_mean True ist. Darüber hinaus berücksichtigt der von precenter subtrahierte Mittelwert keine Stichprobengewichte und korrigiert auch keine Verzerrung aufgrund von konsistent fehlenden Beobachtungen bei Spitzen und/oder Tälern. Wenn der Parameter normalize "amplitude" ist, tendiert die vorhergesagte Amplitude für jede Frequenz in freqs, die kleiner ist als (2*pi)/(x.max() - x.min()), gegen unendlich. Das Konzept einer "Nyquist-Frequenzgrenze" (siehe Nyquist-Shannon-Abtasttheorem) ist für ungleichmäßig abgetastete Daten im Allgemeinen nicht anwendbar. Daher können bei ungleichmäßig abgetasteten Daten gültige Frequenzen in freqs oft viel höher sein als erwartet.

Referenzen

[1]

N.R. Lomb „Least-squares frequency analysis of unequally spaced data“, Astrophysics and Space Science, Bd. 39, S. 447-462, 1976 DOI:10.1007/bf00648343

[2]

J.D. Scargle „Studies in astronomical time series analysis. II - Statistical aspects of spectral analysis of unevenly spaced data“, The Astrophysical Journal, Bd. 263, S. 835-853, 1982 DOI:10.1086/160554

[3]

M. Zechmeister und M. Kürster, „The generalised Lomb-Scargle periodogram. A new formalism for the floating-mean and Keplerian periodograms.“, Astronomy and Astrophysics, Bd. 496, S. 577-584, 2009 DOI:10.1051/0004-6361:200811296

[4]

J.T. VanderPlas, „Understanding the Lomb-Scargle Periodogram.“, The Astrophysical Journal Supplement Series, Bd. 236, Nr. 1, S. 16, Mai 2018 DOI:10.3847/1538-4365/aab766

Beispiele

>>> import numpy as np
>>> rng = np.random.default_rng()

Definieren Sie zunächst einige Eingabeparameter für das Signal

>>> A = 2.  # amplitude
>>> c = 2.  # offset
>>> w0 = 1.  # rad/sec
>>> nin = 150
>>> nout = 1002

Zufällige Erzeugung von Abtastzeiten

>>> x = rng.uniform(0, 10*np.pi, nin)

Plot einer Sinuswelle für die ausgewählten Zeiten

>>> y = A * np.cos(w0*x) + c

Definieren Sie das Frequenzarray, für das das Periodogramm berechnet werden soll

>>> w = np.linspace(0.25, 10, nout)

Berechnen Sie das Lomb-Scargle-Periodogramm für jede der Normalisierungsoptionen

>>> from scipy.signal import lombscargle
>>> pgram_power = lombscargle(x, y, w, normalize=False)
>>> pgram_norm = lombscargle(x, y, w, normalize=True)
>>> pgram_amp = lombscargle(x, y, w, normalize='amplitude')
...
>>> pgram_power_f = lombscargle(x, y, w, normalize=False, floating_mean=True)
>>> pgram_norm_f = lombscargle(x, y, w, normalize=True, floating_mean=True)
>>> pgram_amp_f = lombscargle(x, y, w, normalize='amplitude', floating_mean=True)

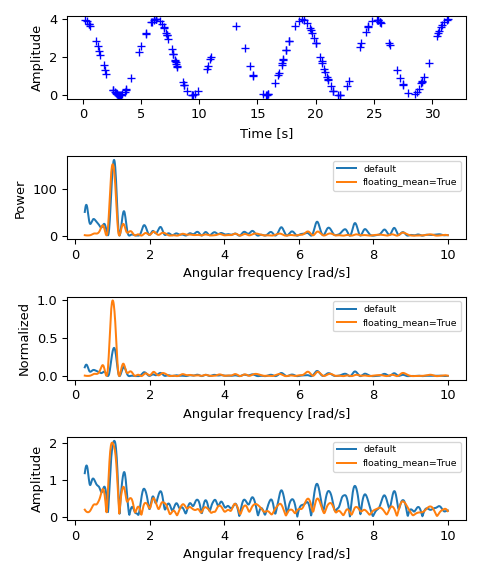
Zeichnen Sie nun ein Diagramm der Eingabedaten

>>> import matplotlib.pyplot as plt
>>> fig, (ax_t, ax_p, ax_n, ax_a) = plt.subplots(4, 1, figsize=(5, 6))
>>> ax_t.plot(x, y, 'b+')
>>> ax_t.set_xlabel('Time [s]')
>>> ax_t.set_ylabel('Amplitude')

Zeichnen Sie dann das Periodogramm für jede der Normalisierungsoptionen sowie mit und ohne floating_mean=True

>>> ax_p.plot(w, pgram_power, label='default')
>>> ax_p.plot(w, pgram_power_f, label='floating_mean=True')
>>> ax_p.set_xlabel('Angular frequency [rad/s]')
>>> ax_p.set_ylabel('Power')
>>> ax_p.legend(prop={'size': 7})
...
>>> ax_n.plot(w, pgram_norm, label='default')
>>> ax_n.plot(w, pgram_norm_f, label='floating_mean=True')
>>> ax_n.set_xlabel('Angular frequency [rad/s]')
>>> ax_n.set_ylabel('Normalized')
>>> ax_n.legend(prop={'size': 7})
...
>>> ax_a.plot(w, np.abs(pgram_amp), label='default')
>>> ax_a.plot(w, np.abs(pgram_amp_f), label='floating_mean=True')
>>> ax_a.set_xlabel('Angular frequency [rad/s]')
>>> ax_a.set_ylabel('Amplitude')
>>> ax_a.legend(prop={'size': 7})
...
>>> plt.tight_layout()
>>> plt.show()

../../_images/scipy-signal-lombscargle-1.png