scipy.signal.

minimum_phase#

scipy.signal.minimum_phase(h, method='homomorphic', n_fft=None, *, half=True)[Quelle]#

Konvertiert einen FIR-Filter mit Linearphase in einen Minimumphasenfilter

Parameter:

harray

Koeffizienten eines FIR-Filters mit Linearphase.

method{‘hilbert’, ‘homomorphic’}

Die bereitgestellten Methoden sind

‘homomorphic’ (Standard)
Diese Methode [4] [5] funktioniert am besten mit Filtern mit einer ungeraden Anzahl von Taps. Der resultierende Minimumphasenfilter hat eine Amplitudenantwort, die ungefähr der Quadratwurzel der Amplitudenantwort des ursprünglichen Filters entspricht, wobei die Hälfte der Taps verwendet wird, wenn half=True (Standard), oder das ursprüngliche Amplitudenspektrum mit der gleichen Anzahl von Taps, wenn half=False.

‘hilbert’
Diese Methode [1] ist für die Verwendung mit Equiripple-Filtern (z. B. aus remez) mit Einheits- oder Nulldurchgangsbereichen konzipiert.

n_fftint

Die Anzahl der Punkte, die für die FFT verwendet werden sollen. Sollte mindestens einige Male größer sein als die Signallänge (siehe Hinweise).

halfbool

Wenn True, wird ein Filter erstellt, der halb so lang ist wie der ursprüngliche, mit einem Amplitudenspektrum, das die Quadratwurzel des ursprünglichen ist. Wenn False, wird ein Filter erstellt, der die gleiche Länge wie der ursprüngliche hat, mit einem Amplitudenspektrum, das so konzipiert ist, dass es dem ursprünglichen entspricht (nur unterstützt, wenn method='homomorphic').

Hinzugefügt in Version 1.14.0.

Rückgabe:

h_minimumarray: Die Minimumphasenversion des Filters mit der Länge (len(h) + 1) // 2, wenn half is True, oder len(h) andernfalls.

Siehe auch

firwin
firwin2
remez

Hinweise

Sowohl die Hilbert- [1] als auch die homomorphe Methode [4] [5] erfordern die Auswahl einer FFT-Länge zur Schätzung des komplexen Cepstrums des Filters.

Im Fall der Hilbert-Methode hängt die Abweichung vom idealen Spektrum epsilon von der Anzahl der Sperrbereichsnullen n_stop und der FFT-Länge n_fft ab, wie folgt:

epsilon = 2. * n_stop / n_fft

Beispielsweise mit 100 Sperrbereichsnullen und einer FFT-Länge von 2048 ist epsilon = 0.0976. Wenn wir konservativ davon ausgehen, dass die Anzahl der Sperrbereichsnullen um eins geringer ist als die Filterlänge, können wir die FFT-Länge als die nächste Zweierpotenz wählen, die epsilon=0.01 erfüllt, wie folgt:

n_fft = 2 ** int(np.ceil(np.log2(2 * (len(h) - 1) / 0.01)))

Dies liefert vernünftige Ergebnisse sowohl für die Hilbert- als auch für die homomorphe Methode und ergibt den Wert, der verwendet wird, wenn n_fft=None.

Es existieren alternative Implementierungen zur Erstellung von Minimumphasenfiltern, darunter Null-Invertierung [2] und spektrale Faktorisierung [3] [4]. Weitere Informationen finden Sie auf dieser DSPGuru-Seite.

Referenzen

[1] (1,2)

N. Damera-Venkata und B. L. Evans, „Optimal design of real and complex minimum phase digital FIR filters,“ Acoustics, Speech, and Signal Processing, 1999. Proceedings., 1999 IEEE International Conference on, Phoenix, AZ, 1999, S. 1145-1148 Bd. 3. DOI:10.1109/ICASSP.1999.756179

[2]

X. Chen und T. W. Parks, „Design of optimal minimum phase FIR filters by direct factorization,“ Signal Processing, Bd. 10, Nr. 4, S. 369-383, Jun. 1986.

[3]

T. Saramaki, „Finite Impulse Response Filter Design,“ in Handbook for Digital Signal Processing, Kapitel 4, New York: Wiley-Interscience, 1993.

[4] (1,2,3)

J. S. Lim, Advanced Topics in Signal Processing. Englewood Cliffs, N.J.: Prentice Hall, 1988.

[5] (1,2)

A. V. Oppenheim, R. W. Schafer und J. R. Buck, „Discrete-Time Signal Processing,“ 3. Auflage. Upper Saddle River, N.J.: Pearson, 2009.

Beispiele

Erstellen Sie einen optimalen Tiefpassfilter mit Linearphase h mit einem Übergangsbereich von [0.2, 0.3] (bei einer Nyquist-Frequenz von 1)

>>> import numpy as np
>>> from scipy.signal import remez, minimum_phase, freqz, group_delay
>>> import matplotlib.pyplot as plt
>>> freq = [0, 0.2, 0.3, 1.0]
>>> desired = [1, 0]
>>> h_linear = remez(151, freq, desired, fs=2)

Konvertieren Sie ihn in Minimumphase

>>> h_hil = minimum_phase(h_linear, method='hilbert')
>>> h_hom = minimum_phase(h_linear, method='homomorphic')
>>> h_hom_full = minimum_phase(h_linear, method='homomorphic', half=False)

Vergleichen Sie die Impuls- und Frequenzantwort der vier Filter

>>> fig0, ax0 = plt.subplots(figsize=(6, 3), tight_layout=True)
>>> fig1, axs = plt.subplots(3, sharex='all', figsize=(6, 6), tight_layout=True)
>>> ax0.set_title("Impulse response")
>>> ax0.set(xlabel='Samples', ylabel='Amplitude', xlim=(0, len(h_linear) - 1))
>>> axs[0].set_title("Frequency Response")
>>> axs[0].set(xlim=(0, .65), ylabel="Magnitude / dB")
>>> axs[1].set(ylabel="Phase / rad")
>>> axs[2].set(ylabel="Group Delay / samples", ylim=(-31, 81),
...             xlabel='Normalized Frequency (Nyqist frequency: 1)')
>>> for h, lb in ((h_linear,   f'Linear ({len(h_linear)})'),
...               (h_hil,      f'Min-Hilbert ({len(h_hil)})'),
...               (h_hom,      f'Min-Homomorphic ({len(h_hom)})'),
...               (h_hom_full, f'Min-Homom. Full ({len(h_hom_full)})')):
...     w_H, H = freqz(h, fs=2)
...     w_gd, gd = group_delay((h, 1), fs=2)
...
...     alpha = 1.0 if lb == 'linear' else 0.5  # full opacity for 'linear' line
...     ax0.plot(h, '.-', alpha=alpha, label=lb)
...     axs[0].plot(w_H, 20 * np.log10(np.abs(H)), alpha=alpha)
...     axs[1].plot(w_H, np.unwrap(np.angle(H)), alpha=alpha, label=lb)
...     axs[2].plot(w_gd, gd, alpha=alpha)
>>> ax0.grid(True)
>>> ax0.legend(title='Filter Phase (Order)')
>>> axs[1].legend(title='Filter Phase (Order)', loc='lower right')
>>> for ax_ in axs:  # shade transition band:
...     ax_.axvspan(freq[1], freq[2], color='y', alpha=.25)
...     ax_.grid(True)
>>> plt.show()

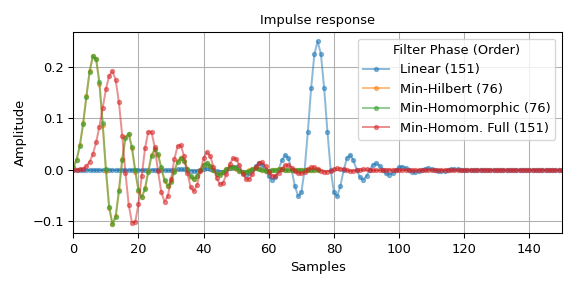
../../_images/scipy-signal-minimum_phase-1_00_00.png

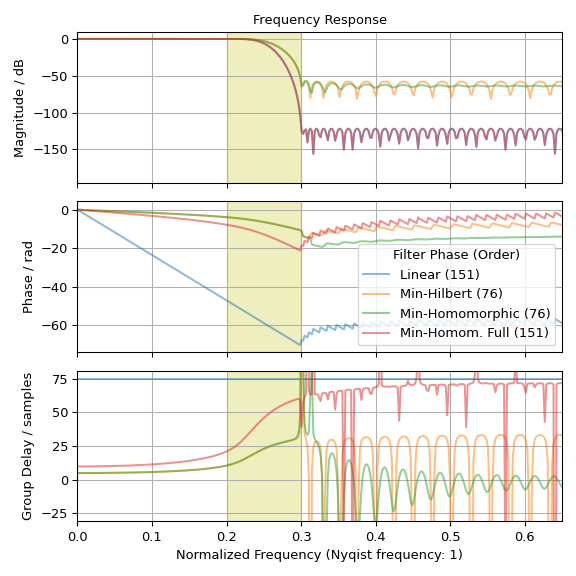
../../_images/scipy-signal-minimum_phase-1_00_01.png

Die Impulsantwort- und Gruppenlaufzeit-Diagramme zeigen die Verzögerung von 75 Samples des Linearphasenfilters h. Die Phase sollte im Sperrbereich ebenfalls linear sein – aufgrund der geringen Amplitude dominiert dort numerisches Rauschen. Darüber hinaus zeigen die Diagramme, dass die Minimumphasenfilter eine klar reduzierte (negative) Phasensteigung im Durchlass- und Übergangsbereich aufweisen. Die Diagramme veranschaulichen auch, dass der Filter mit den Parametern method='homomorphic', half=False die gleiche Ordnung und Amplitudenantwort wie der lineare Filter h hat, während die anderen Minimumphasenfilter nur die halbe Ordnung und die Quadratwurzel der Amplitudenantwort haben.