scipy.signal.

place_poles#

scipy.signal.place_poles(A, B, poles, method='YT', rtol=0.001, maxiter=30)[Quelle]#

Berechnet K sodass die Eigenwerte von (A - dot(B, K)) = poles sind.

K ist die Verstärkungsmatrix, so dass das durch das Liniensystem AX+BU beschriebene System seine geschlossenen Polstellen, d. h. die Eigenwerte von A - B*K, so nah wie möglich an die in poles gewünschten Werte bringt.

SISO-, MISO- und MIMO-Systeme werden unterstützt.

Parameter:

A, Bndarray

Zustandsraumdarstellung des linearen Systems AX + BU.

polesarray_like

Gewünschte reelle Polstellen und/oder komplexe konjugierte Polstellen. Komplexe Polstellen werden nur mit method="YT" (Standard) unterstützt.

method: {‘YT’, ‘KNV0’}, optional

Welche Methode zur Berechnung der Verstärkungsmatrix K gewählt werden soll. Eine von

‘YT’: Yang Tits

‘KNV0’: Kautsky, Nichols, Van Dooren Update-Methode 0

Siehe Referenzen und Hinweise für Details zu den Algorithmen.

rtol: float, optional

Nach jeder Iteration wird die Determinante der Eigenvektoren von A - B*K mit ihrem vorherigen Wert verglichen. Wenn der relative Fehler zwischen diesen beiden Werten kleiner als rtol ist, stoppt der Algorithmus. Standard ist 1e-3.

maxiter: int, optional

Maximale Anzahl von Iterationen zur Berechnung der Verstärkungsmatrix. Standard ist 30.

Rückgabe:

full_state_feedbackBunch object

full_state_feedback besteht aus

gain_matrix1-D ndarray: Die geschlossene Schleifenmatrix K, so dass die Eigenwerte von A-BK so nah wie möglich an die angeforderten Polstellen heranreichen.
computed_poles1-D ndarray: Die Polstellen, die zu A-BK gehören, sortiert zuerst nach reellen Polstellen in aufsteigender Reihenfolge, dann nach komplexen konjugierten Polstellen in lexikographischer Reihenfolge.
requested_poles1-D ndarray: Die Polstellen, die der Algorithmus zu platzieren hatte, sortiert wie oben. Sie können von dem erreichten Ergebnis abweichen.
X2-D ndarray: Die Übertragungsmatrix, so dass X * diag(poles) = (A - B*K)*X (siehe Hinweise)
rtolfloat: Die relative Toleranz, die bei det(X) erreicht wurde (siehe Hinweise). rtol ist NaN, wenn das System diag(poles) = (A - B*K) gelöst werden kann, oder 0, wenn die Optimierungsalgorithmen nichts tun können, d. h. wenn B.shape[1] == 1.
nb_iterint: Die Anzahl der Iterationen, die vor der Konvergenz durchgeführt wurden. nb_iter ist NaN, wenn das System diag(poles) = (A - B*K) gelöst werden kann, oder 0, wenn die Optimierungsalgorithmen nichts tun können, d. h. wenn B.shape[1] == 1.

Hinweise

Das Papier von Tits und Yang (YT) [2] ist eine Aktualisierung des ursprünglichen Papiers von Kautsky et al. (KNV) [1]. KNV basiert auf Rang-1-Updates, um die Übertragungsmatrix X zu finden, so dass X * diag(poles) = (A - B*K)*X, während YT Rang-2-Updates verwendet. Dies liefert im Durchschnitt robustere Lösungen (siehe [2] S. 21-22). Darüber hinaus unterstützt der YT-Algorithmus komplexe Polstellen, während KNV in seiner ursprünglichen Version dies nicht tut. Nur die von KNV vorgeschlagene Update-Methode 0 wurde hier implementiert, daher der Name 'KNV0'.

KNV, erweitert um komplexe Polstellen, wird in Matlabs place-Funktion verwendet. YT wird unter einer nicht-freien Lizenz von Slicot unter dem Namen robpole vertrieben. Es ist unklar und undokumentiert, wie KNV0 auf komplexe Polstellen erweitert wurde (Tits und Yang behaupten auf Seite 14 ihres Papiers, dass ihre Methode nicht zur Erweiterung von KNV auf komplexe Polstellen verwendet werden kann). Daher unterstützen nur YT diese in dieser Implementierung.

Da die Lösung des Problems der Polstellenplatzierung für MIMO-Systeme nicht eindeutig ist, beginnen beide Methoden mit einer vorläufigen Übertragungsmatrix, die auf verschiedene Weise geändert wird, um ihre Determinante zu erhöhen. Beide Methoden konvergieren nachweislich zu einer stabilen Lösung. Abhängig von der Wahl der anfänglichen Übertragungsmatrix konvergieren sie jedoch zu unterschiedlichen Lösungen, und es gibt absolut keine Garantie dafür, dass die Verwendung von 'KNV0' zu ähnlichen Ergebnissen wie Matlab oder einer anderen Implementierung dieser Algorithmen führt.

Die Verwendung der Standardmethode 'YT' sollte in den meisten Fällen in Ordnung sein. 'KNV0' wird nur bereitgestellt, da sie in einigen spezifischen Fällen von 'YT' benötigt wird. Darüber hinaus liefert 'YT' im Durchschnitt robustere Ergebnisse als 'KNV0', wenn abs(det(X)) als Robustheitsindikator verwendet wird.

[2] ist als technischer Bericht unter der folgenden URL verfügbar: https://hdl.handle.net/1903/5598

Referenzen

[1] (1,2)

J. Kautsky, N.K. Nichols und P. van Dooren, „Robust pole assignment in linear state feedback“, International Journal of Control, Bd. 41, S. 1129-1155, 1985.

[2] (1,2,3)

A.L. Tits und Y. Yang, „Globally convergent algorithms for robust pole assignment by state feedback“, IEEE Transactions on Automatic Control, Bd. 41, S. 1432-1452, 1996.

Beispiele

Ein einfaches Beispiel zur Demonstration der Platzierung reeller Polstellen mit den Algorithmen KNV und YT. Dies ist Beispiel 1 aus Abschnitt 4 der Referenzpublikation KNV ([1])

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> A = np.array([[ 1.380,  -0.2077,  6.715, -5.676  ],
...               [-0.5814, -4.290,   0,      0.6750 ],
...               [ 1.067,   4.273,  -6.654,  5.893  ],
...               [ 0.0480,  4.273,   1.343, -2.104  ]])
>>> B = np.array([[ 0,      5.679 ],
...               [ 1.136,  1.136 ],
...               [ 0,      0,    ],
...               [-3.146,  0     ]])
>>> P = np.array([-0.2, -0.5, -5.0566, -8.6659])

Berechnen Sie nun K mit der KNV-Methode 0, mit der Standard-YT-Methode und mit der YT-Methode, wobei 100 Iterationen des Algorithmus erzwungen werden, und geben Sie nach jedem Aufruf einige Ergebnisse aus.

>>> fsf1 = signal.place_poles(A, B, P, method='KNV0')
>>> fsf1.gain_matrix
array([[ 0.20071427, -0.96665799,  0.24066128, -0.10279785],
       [ 0.50587268,  0.57779091,  0.51795763, -0.41991442]])

>>> fsf2 = signal.place_poles(A, B, P)  # uses YT method
>>> fsf2.computed_poles
array([-8.6659, -5.0566, -0.5   , -0.2   ])

>>> fsf3 = signal.place_poles(A, B, P, rtol=-1, maxiter=100)
>>> fsf3.X
array([[ 0.52072442+0.j, -0.08409372+0.j, -0.56847937+0.j,  0.74823657+0.j],
       [-0.04977751+0.j, -0.80872954+0.j,  0.13566234+0.j, -0.29322906+0.j],
       [-0.82266932+0.j, -0.19168026+0.j, -0.56348322+0.j, -0.43815060+0.j],
       [ 0.22267347+0.j,  0.54967577+0.j, -0.58387806+0.j, -0.40271926+0.j]])

Der Absolutwert der Determinante von X ist ein guter Indikator, um die Robustheit der Ergebnisse zu überprüfen. Sowohl 'KNV0' als auch 'YT' zielen darauf ab, ihn zu maximieren. Unten ein Vergleich der Robustheit der obigen Ergebnisse

>>> abs(np.linalg.det(fsf1.X)) < abs(np.linalg.det(fsf2.X))
True
>>> abs(np.linalg.det(fsf2.X)) < abs(np.linalg.det(fsf3.X))
True

Nun ein einfaches Beispiel für komplexe Polstellen

>>> A = np.array([[ 0,  7/3.,  0,   0   ],
...               [ 0,   0,    0,  7/9. ],
...               [ 0,   0,    0,   0   ],
...               [ 0,   0,    0,   0   ]])
>>> B = np.array([[ 0,  0 ],
...               [ 0,  0 ],
...               [ 1,  0 ],
...               [ 0,  1 ]])
>>> P = np.array([-3, -1, -2-1j, -2+1j]) / 3.
>>> fsf = signal.place_poles(A, B, P, method='YT')

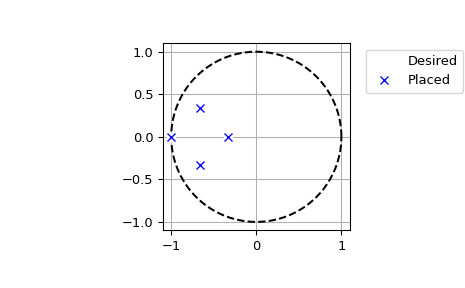
Wir können die gewünschten und berechneten Polstellen in der komplexen Ebene darstellen

>>> t = np.linspace(0, 2*np.pi, 401)
>>> plt.plot(np.cos(t), np.sin(t), 'k--')  # unit circle
>>> plt.plot(fsf.requested_poles.real, fsf.requested_poles.imag,
...          'wo', label='Desired')
>>> plt.plot(fsf.computed_poles.real, fsf.computed_poles.imag, 'bx',
...          label='Placed')
>>> plt.grid()
>>> plt.axis('image')
>>> plt.axis([-1.1, 1.1, -1.1, 1.1])
>>> plt.legend(bbox_to_anchor=(1.05, 1), loc=2, numpoints=1)

../../_images/scipy-signal-place_poles-1.png