resample_poly#
- scipy.signal.resample_poly(x, up, down, axis=0, window=('kaiser', 5.0), padtype='constant', cval=None)[Quelle]#
Resampelt x entlang der angegebenen Achse mittels Polyphasenfilterung.
Das Signal x wird um den Faktor up hochgetastet, ein Tiefpass-FIR-Filter mit Nullphasenverzögerung wird angewendet, und dann wird es um den Faktor down heruntergetastet. Die resultierende Abtastrate ist
up / downmal die ursprüngliche Abtastrate. Standardmäßig werden Werte außerhalb des Signalrands während des Filterungsschritts als Null angenommen.- Parameter:
- xarray_like
Die zu resampelnden Daten.
- upint
Der Hochtastfaktor.
- downint
Der Heruntertastfaktor.
- axisint, optional
Die Achse von x, die resampelt wird. Standard ist 0.
- windowstring, tuple, oder array_like, optional
Das zu verwendende Fenster zur Entwurfs des Tiefpassfilters oder die zu verwendenden FIR-Filterkoeffizienten. Siehe unten für Details.
- padtypestring, optional
constant, line, mean, median, maximum, minimum oder jeder der anderen Signalverlängerungsmodi, die von
scipy.signal.upfirdnunterstützt werden. Ändert Annahmen über Werte außerhalb des Rands. Wenn constant, wird angenommen, dass sie cval (Standard Null) sind. Wenn line, wird angenommen, dass sie einen linearen Trend fortsetzen, der durch den ersten und letzten Punkt definiert ist. mean, median, maximum und minimum funktionieren wie in np.pad und nehmen an, dass die Werte außerhalb des Rands der Mittelwert, Median, das Maximum oder Minimum des Arrays entlang der Achse sind.Hinzugefügt in Version 1.4.0.
- cvalfloat, optional
Wert, der verwendet wird, wenn padtype=’constant’. Standard ist Null.
Hinzugefügt in Version 1.4.0.
- Rückgabe:
- resampled_xarray
Das resampelte Array.
Siehe auch
Hinweise
Diese Polyphasenmethode ist wahrscheinlich schneller als die Fourier-Methode in
scipy.signal.resample, wenn die Anzahl der Samples groß und prim ist, oder wenn die Anzahl der Samples groß ist und up und down einen großen gemeinsamen Teiler haben. Die Länge des verwendeten FIR-Filters hängt vonmax(up, down) // gcd(up, down)ab, und die Anzahl der Operationen während der Polyphasenfilterung hängt von der Filterlänge und down ab (siehescipy.signal.upfirdnfür Details).Das Argument window gibt den Entwurf des FIR-Tiefpassfilters an.
Wenn window ein Array-ähnliches Objekt ist, wird angenommen, dass es sich um die FIR-Filterkoeffizienten handelt. Beachten Sie, dass der FIR-Filter nach dem Hochtastschritt angewendet wird, sodass er für die Verarbeitung eines Signals mit einer Abtastfrequenz ausgelegt sein sollte, die um den Faktor up//gcd(up, down) höher ist als die ursprüngliche. Die Ausgabe dieser Funktion wird relativ zu diesem Array zentriert sein, daher ist es am besten, einen symmetrischen Filter mit einer ungeraden Anzahl von Samples zu übergeben, wenn, wie üblich, ein Nullphasenfilter gewünscht wird.
Für jeden anderen Typ von window werden die Funktionen
scipy.signal.get_windowundscipy.signal.firwinaufgerufen, um die entsprechenden Filterkoeffizienten zu generieren.Das erste Sample des zurückgegebenen Vektors ist dasselbe wie das erste Sample des Eingangsvektors. Der Abstand zwischen den Samples ändert sich von
dxzudx * down / float(up).Beispiele
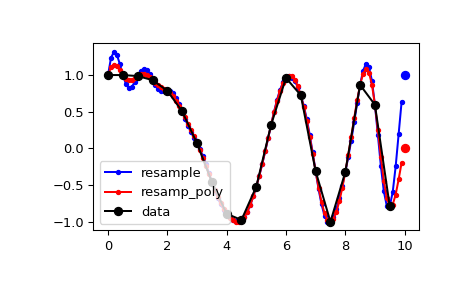
Standardmäßig steigt das Ende der resampelten Daten, um das erste Sample des nächsten Zyklus für die FFT-Methode zu erreichen, und nähert sich Null für die Polyphasenmethode
>>> import numpy as np >>> from scipy import signal >>> import matplotlib.pyplot as plt
>>> x = np.linspace(0, 10, 20, endpoint=False) >>> y = np.cos(-x**2/6.0) >>> f_fft = signal.resample(y, 100) >>> f_poly = signal.resample_poly(y, 100, 20) >>> xnew = np.linspace(0, 10, 100, endpoint=False)
>>> plt.plot(xnew, f_fft, 'b.-', xnew, f_poly, 'r.-') >>> plt.plot(x, y, 'ko-') >>> plt.plot(10, y[0], 'bo', 10, 0., 'ro') # boundaries >>> plt.legend(['resample', 'resamp_poly', 'data'], loc='best') >>> plt.show()
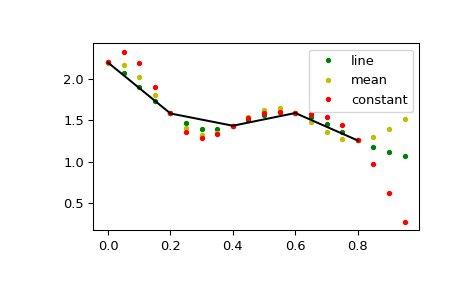
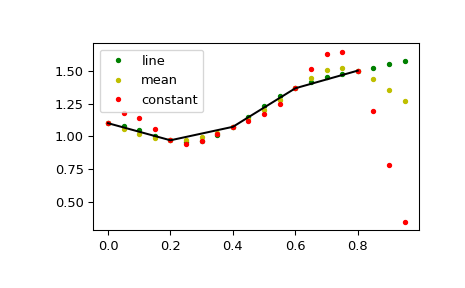
Dieses Standardverhalten kann durch die Option padtype geändert werden
>>> N = 5 >>> x = np.linspace(0, 1, N, endpoint=False) >>> y = 2 + x**2 - 1.7*np.sin(x) + .2*np.cos(11*x) >>> y2 = 1 + x**3 + 0.1*np.sin(x) + .1*np.cos(11*x) >>> Y = np.stack([y, y2], axis=-1) >>> up = 4 >>> xr = np.linspace(0, 1, N*up, endpoint=False)
>>> y2 = signal.resample_poly(Y, up, 1, padtype='constant') >>> y3 = signal.resample_poly(Y, up, 1, padtype='mean') >>> y4 = signal.resample_poly(Y, up, 1, padtype='line')
>>> for i in [0,1]: ... plt.figure() ... plt.plot(xr, y4[:,i], 'g.', label='line') ... plt.plot(xr, y3[:,i], 'y.', label='mean') ... plt.plot(xr, y2[:,i], 'r.', label='constant') ... plt.plot(x, Y[:,i], 'k-') ... plt.legend() >>> plt.show()