scipy.signal.windows.

exponential

scipy.signal.windows.exponential(M, center=None, tau=1.0, sym=True, *, xp=None, device=None)

Gibt ein exponentielles (oder Poisson-) Fenster zurück.

Parameter:

Mint

Anzahl der Punkte im Ausgabefenster. Wenn Null, wird ein leeres Array zurückgegeben. Bei negativen Werten wird eine Ausnahme ausgelöst.

centerfloat, optional

Parameter, der die Position des Zentrums der Fensterfunktion definiert. Der Standardwert, wenn nicht angegeben, ist center = (M-1) / 2. Dieser Parameter muss seinen Standardwert für symmetrische Fenster annehmen.

taufloat, optional

Parameter, der den Zerfall definiert. Für center = 0 verwenden Sie tau = -(M-1) / ln(x), wenn x der verbleibende Bruchteil des Fensters am Ende ist.

symbool, optional

Wenn True (Standard), wird ein symmetrisches Fenster zur Filterentwurf verwendet. Wenn False, wird ein periodisches Fenster für die Spektralanalyse generiert.

xparray_namespace, optional

Optionaler Array-Namespace. Sollte mit dem Array-API-Standard kompatibel sein oder von array-api-compat unterstützt werden. Standard: numpy

device: any

optionale Gerätespezifikation für die Ausgabe. Sollte mit einer der unterstützten Gerätespezifikationen in xp übereinstimmen.

Rückgabe:

wndarray

Das Fenster, dessen Maximalwert auf 1 normiert ist (obwohl der Wert 1 nicht erscheint, wenn M gerade und sym True ist).

Hinweise

Das exponentielle Fenster ist definiert als

\[w(n) = e^{-|n-center| / \tau}\]

Referenzen

[1]

S. Gade und H. Herlufsen, „Windows to FFT analysis (Part I)“, Technical Review 3, Bruel & Kjaer, 1987.

Beispiele

Probieren Sie es in Ihrem Browser aus!

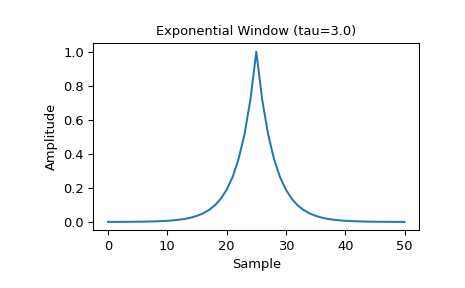
Plotten Sie das symmetrische Fenster und seine Frequenzantwort

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> M = 51
>>> tau = 3.0
>>> window = signal.windows.exponential(M, tau=tau)
>>> plt.plot(window)
>>> plt.title("Exponential Window (tau=3.0)")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

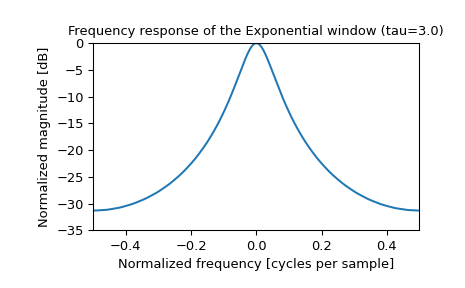
>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -35, 0])
>>> plt.title("Frequency response of the Exponential window (tau=3.0)")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")

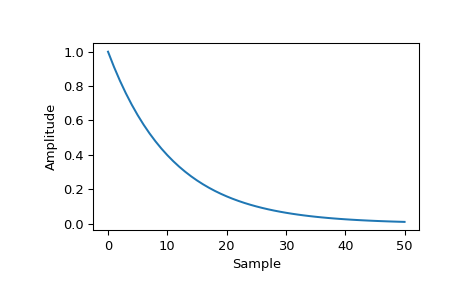
Diese Funktion kann auch nicht-symmetrische Fenster erzeugen

>>> tau2 = -(M-1) / np.log(0.01)
>>> window2 = signal.windows.exponential(M, 0, tau2, False)
>>> plt.figure()
>>> plt.plot(window2)
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

ZurückIn Tab öffnen