kaiser#
- scipy.signal.windows.kaiser(M, beta, sym=True, *, xp=None, device=None)[Quelle]#
Gibt ein Kaiser-Fenster zurück.
Das Kaiser-Fenster ist ein sich verjüngendes Fenster, das durch Verwendung einer Bessel-Funktion gebildet wird.
- Parameter:
- Mint
Anzahl der Punkte im Ausgabefenster. Wenn Null, wird ein leeres Array zurückgegeben. Bei negativen Werten wird eine Ausnahme ausgelöst.
- betafloat
Formparameter, der den Kompromiss zwischen Hauptkeulenbreite und Nebenkeulenpegel bestimmt. Wenn Beta größer wird, wird das Fenster schmaler.
- symbool, optional
Wenn True (Standard), wird ein symmetrisches Fenster zur Filterentwurf verwendet. Wenn False, wird ein periodisches Fenster für die Spektralanalyse generiert.
- xparray_namespace, optional
Optionaler Array-Namespace. Sollte mit dem Array-API-Standard kompatibel sein oder von array-api-compat unterstützt werden. Standard:
numpy- device: any
optionale Gerätespezifikation für die Ausgabe. Sollte mit einer der unterstützten Gerätespezifikationen in
xpübereinstimmen.
- Rückgabe:
- wndarray
Das Fenster, dessen Maximalwert auf 1 normiert ist (obwohl der Wert 1 nicht erscheint, wenn M gerade und sym True ist).
Hinweise
Das Kaiser-Fenster ist definiert als
\[w(n) = I_0\left( \beta \sqrt{1-\frac{4n^2}{(M-1)^2}} \right)/I_0(\beta)\]mit
\[\quad -\frac{M-1}{2} \leq n \leq \frac{M-1}{2},\]wobei \(I_0\) die modifizierte Bessel-Funktion der Ordnung null ist.
Das Kaiser-Fenster wurde nach Jim Kaiser benannt, der eine einfache Annäherung an das DPSS-Fenster (Discrete Prolate Spheroidal Sequence) basierend auf Bessel-Funktionen entdeckte. Das Kaiser-Fenster ist eine sehr gute Annäherung an die diskrete prolaten sphärische Sequenz, oder das Slepian-Fenster, welches die Transformation ist, die die Energie in der Hauptkeule des Fensters im Verhältnis zur Gesamtenergie maximiert.
Das Kaiser-Fenster kann andere Fenster durch Variation des Beta-Parameters annähern. (Einige Literatur verwendet alpha = beta/pi.) [4]
beta
Fensterform
0
Rechteckig
5
Ähnlich einem Hamming-Fenster
6
Ähnlich einem Hann-Fenster
8.6
Ähnlich einem Blackman-Fenster
Ein Beta-Wert von 14 ist wahrscheinlich ein guter Ausgangspunkt. Beachten Sie, dass, wenn Beta größer wird, das Fenster schmaler wird und daher die Anzahl der Abtastpunkte groß genug sein muss, um die sich immer weiter verengende Spitze abzutasten, andernfalls werden NaNs zurückgegeben.
Die meisten Bezüge zum Kaiser-Fenster stammen aus der Signalverarbeitungsliteratur, wo es als eine von vielen Fensterfunktionen zum Glätten von Werten verwendet wird. Es ist auch als Apodisationsfunktion (was bedeutet „den Fuß entfernen“, d.h. Glätten von Diskontinuitäten am Anfang und Ende des abgetasteten Signals) oder als Verjüngungsfunktion bekannt.
Referenzen
[1]J. F. Kaiser, „Digital Filters“ – Kapitel 7 in „Systems analysis by digital computer“, Herausgeber: F.F. Kuo und J.F. Kaiser, S. 218-285. John Wiley and Sons, New York, (1966).
[2]E.R. Kanasewich, „Time Sequence Analysis in Geophysics“, The University of Alberta Press, 1975, S. 177-178.
[3]Wikipedia, „Fensterfunktion“, https://en.wikipedia.org/wiki/Window_function
[4]F. J. Harris, „On the use of windows for harmonic analysis with the discrete Fourier transform,“ Proceedings of the IEEE, Bd. 66, Nr. 1, S. 51-83, Jan. 1978. DOI:10.1109/PROC.1978.10837.
Beispiele
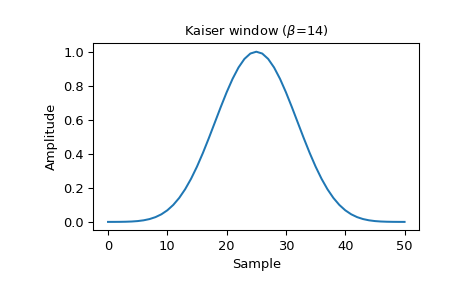
Plotten Sie das Fenster und seine Frequenzantwort
>>> import numpy as np >>> from scipy import signal >>> from scipy.fft import fft, fftshift >>> import matplotlib.pyplot as plt
>>> window = signal.windows.kaiser(51, beta=14) >>> plt.plot(window) >>> plt.title(r"Kaiser window ($\beta$=14)") >>> plt.ylabel("Amplitude") >>> plt.xlabel("Sample")
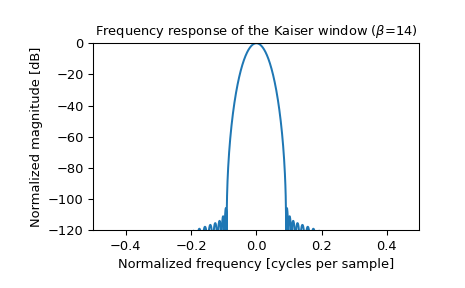
>>> plt.figure() >>> A = fft(window, 2048) / (len(window)/2.0) >>> freq = np.linspace(-0.5, 0.5, len(A)) >>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max()))) >>> plt.plot(freq, response) >>> plt.axis([-0.5, 0.5, -120, 0]) >>> plt.title(r"Frequency response of the Kaiser window ($\beta$=14)") >>> plt.ylabel("Normalized magnitude [dB]") >>> plt.xlabel("Normalized frequency [cycles per sample]")