scipy.spatial.

HalfspaceIntersection

class scipy.spatial.HalfspaceIntersection(halfspaces, interior_point, incremental=False, qhull_options=None)

Halbraum-Durchschnitte in N Dimensionen.

Hinzugefügt in Version 0.19.0.

Parameter:

halfspacesndarray von floats, Form (neunq, ndim+1)

Gestapelte Ungleichungen der Form Ax + b <= 0 im Format [A; b]

interior_pointndarray von floats, Form (ndim,)

Punkt, der sich deutlich innerhalb des durch die Halbräume definierten Bereichs befindet. Auch als zulässiger Punkt bezeichnet, kann er durch lineare Programmierung ermittelt werden.

incrementalbool, optional

Ermöglicht das inkrementelle Hinzufügen neuer Halbräume. Dies erfordert einige zusätzliche Ressourcen.

qhull_optionsstr, optional

Zusätzliche Optionen, die an Qhull übergeben werden. Details finden Sie im Qhull-Handbuch. (Standard: „Qx“ für ndim > 4 und „“ andernfalls) Die Option „H“ ist immer aktiviert.

Attribute:

halfspacesndarray von double, Form (neunq, ndim+1)

Eingabe-Halbräume.

interior_point : ndarray von floats, Form (ndim,)

Eingabe-Innenpunkt.

intersectionsndarray von double, Form (ninter, ndim)

Durchschnitte aller Halbräume.

dual_pointsndarray von double, Form (neunq, ndim)

Duale Punkte der Eingabe-Halbräume.

dual_facetsListe von Listen von ints

Indizes von Punkten, die die (nicht notwendigerweise simplizialen) Facetten der dualen konvexen Hülle bilden.

dual_verticesndarray von ints, Form (nvertices,)

Indizes von Halbräumen, die die Ecken der dualen konvexen Hülle bilden. Bei 2D-konvexen Hüllen sind die Ecken gegen den Uhrzeigersinn angeordnet. In anderen Dimensionen sind sie in der Eingabereihenfolge.

dual_equationsndarray von double, Form (nfacet, ndim+1)

[Normalenvektor, Offset], der die Hyperebenengleichung der dualen Facette bildet (siehe Qhull-Dokumentation für weitere Informationen).

dual_areafloat

Fläche der dualen konvexen Hülle

dual_volumefloat

Volumen der dualen konvexen Hülle

Methoden

add_halfspaces(halfspaces[, restart])	Verarbeitet einen Satz zusätzlicher neuer Halbräume.
close()	Beendet die schrittweise Verarbeitung.

Löst aus:

QhullError

Wird ausgelöst, wenn Qhull auf eine Fehlerbedingung stößt, z. B. eine geometrische Degeneration, wenn keine Optionen zur Behebung aktiviert sind.

ValueError

Wird ausgelöst, wenn ein inkompatibles Array als Eingabe gegeben wird.

Hinweise

Die Durchschnitte werden unter Verwendung der Qhull-Bibliothek berechnet. Dies reproduziert die „qhalf“-Funktionalität von Qhull.

Referenzen

[Qhull]

http://www.qhull.org/

[1]

S. Boyd, L. Vandenberghe, Convex Optimization, verfügbar unter http://stanford.edu/~boyd/cvxbook/

Beispiele

Probieren Sie es in Ihrem Browser aus!

Halbraum-Durchschnitt von Ebenen, die ein Polygon bilden

>>> from scipy.spatial import HalfspaceIntersection
>>> import numpy as np
>>> halfspaces = np.array([[-1, 0., 0.],
...                        [0., -1., 0.],
...                        [2., 1., -4.],
...                        [-0.5, 1., -2.]])
>>> feasible_point = np.array([0.5, 0.5])
>>> hs = HalfspaceIntersection(halfspaces, feasible_point)

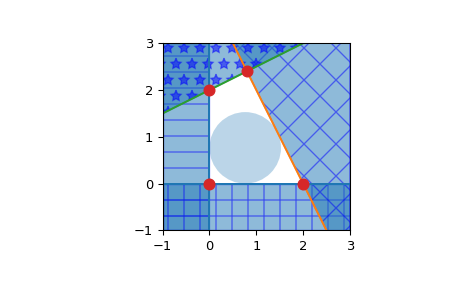
Halbräume als gefüllte Bereiche und Schnittpunkte darstellen

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(1, 1, 1, aspect='equal')
>>> xlim, ylim = (-1, 3), (-1, 3)
>>> ax.set_xlim(xlim)
>>> ax.set_ylim(ylim)
>>> x = np.linspace(-1, 3, 100)
>>> symbols = ['-', '+', 'x', '*']
>>> signs = [0, 0, -1, -1]
>>> fmt = {"color": None, "edgecolor": "b", "alpha": 0.5}
>>> for h, sym, sign in zip(halfspaces, symbols, signs):
...     hlist = h.tolist()
...     fmt["hatch"] = sym
...     if h[1]== 0:
...         ax.axvline(-h[2]/h[0], label='{}x+{}y+{}=0'.format(*hlist))
...         xi = np.linspace(xlim[sign], -h[2]/h[0], 100)
...         ax.fill_between(xi, ylim[0], ylim[1], **fmt)
...     else:
...         ax.plot(x, (-h[2]-h[0]*x)/h[1], label='{}x+{}y+{}=0'.format(*hlist))
...         ax.fill_between(x, (-h[2]-h[0]*x)/h[1], ylim[sign], **fmt)
>>> x, y = zip(*hs.intersections)
>>> ax.plot(x, y, 'o', markersize=8)

Standardmäßig bietet qhull keine Möglichkeit, einen Innenpunkt zu berechnen. Dieser kann leicht durch lineare Programmierung ermittelt werden. Betrachten wir Halbräume der Form \(Ax + b \leq 0\), dann ergibt die Lösung des linearen Programms

\[ \begin{align}\begin{aligned}max \: y\\s.t. Ax + y ||A_i|| \leq -b\end{aligned}\end{align} \]

mit \(A_i\) als Zeilen von A, d.h. den Normalen jeder Ebene.

ergibt einen Punkt x, der am weitesten im konvexen Polyeder liegt. Genauer gesagt ist es das Zentrum der größten Hypersphäre mit Radius y, die in das Polyeder einbeschrieben ist. Dieser Punkt wird als Chebyshev-Zentrum des Polyeders bezeichnet (siehe [1] 4.3.1, S. 148-149). Die von Qhull ausgegebenen Gleichungen sind immer normalisiert.

>>> from scipy.optimize import linprog
>>> from matplotlib.patches import Circle
>>> norm_vector = np.reshape(np.linalg.norm(halfspaces[:, :-1], axis=1),
...     (halfspaces.shape[0], 1))
>>> c = np.zeros((halfspaces.shape[1],))
>>> c[-1] = -1
>>> A = np.hstack((halfspaces[:, :-1], norm_vector))
>>> b = - halfspaces[:, -1:]
>>> res = linprog(c, A_ub=A, b_ub=b, bounds=(None, None))
>>> x = res.x[:-1]
>>> y = res.x[-1]
>>> circle = Circle(x, radius=y, alpha=0.3)
>>> ax.add_patch(circle)
>>> plt.legend(bbox_to_anchor=(1.6, 1.0))
>>> plt.show()

ZurückIn Tab öffnen