scipy.spatial.KDTree.

query_ball_tree

KDTree.query_ball_tree(other, r, p=2.0, eps=0)

Findet alle Punktpaare zwischen self und other, deren Abstand höchstens r beträgt.

Parameter:

otherKDTree-Instanz

Der Baum, der die zu durchsuchenden Punkte enthält.

rFloat

Der maximale Abstand, muss positiv sein.

pfloat, optional

Welche Minkowski-Norm verwendet werden soll. p muss die Bedingung 1 <= p <= infinity erfüllen.

epsfloat, optional

Ungefähre Suche. Äste des Baumes werden nicht erkundet, wenn ihre nächsten Punkte weiter entfernt sind als r/(1+eps), und Äste werden gesammelt hinzugefügt, wenn ihre entferntesten Punkte näher als r * (1+eps) sind. eps muss nicht-negativ sein.

Rückgabe:

resultsListe von Listen

Für jedes Element self.data[i] dieses Baumes ist results[i] eine Liste der Indizes seiner Nachbarn in other.data.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Sie können alle Punktpaare zwischen zwei kd-Bäumen innerhalb eines bestimmten Abstands durchsuchen

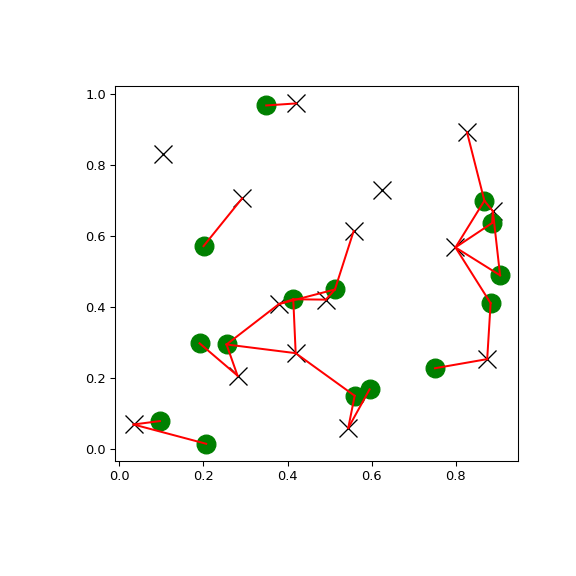
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.spatial import KDTree
>>> rng = np.random.default_rng()
>>> points1 = rng.random((15, 2))
>>> points2 = rng.random((15, 2))
>>> plt.figure(figsize=(6, 6))
>>> plt.plot(points1[:, 0], points1[:, 1], "xk", markersize=14)
>>> plt.plot(points2[:, 0], points2[:, 1], "og", markersize=14)
>>> kd_tree1 = KDTree(points1)
>>> kd_tree2 = KDTree(points2)
>>> indexes = kd_tree1.query_ball_tree(kd_tree2, r=0.2)
>>> for i in range(len(indexes)):
...     for j in indexes[i]:
...         plt.plot([points1[i, 0], points2[j, 0]],
...             [points1[i, 1], points2[j, 1]], "-r")
>>> plt.show()

ZurückIn Tab öffnen