scipy.spatial.

SphericalVoronoi#

class scipy.spatial.SphericalVoronoi(points, radius=1, center=None, threshold=1e-06)[Quelle]#

Voronoi-Diagramme auf der Oberfläche einer Sphäre.

Hinzugefügt in Version 0.18.0.

Parameter:

pointsndarray von floats, Form (npoints, ndim): Koordinaten der Punkte, aus denen ein sphärisches Voronoi-Diagramm konstruiert werden soll.
radiusfloat, optional: Radius der Sphäre (Standard: 1)
centerndarray von floats, Form (ndim,): Mittelpunkt der Sphäre (Standard: Ursprung)
thresholdfloat: Schwellenwert für die Erkennung von doppelten Punkten und Diskrepanzen zwischen Punkten und Sphärenparametern. (Standard: 1e-06)

Attribute:

pointsdouble Array der Form (npoints, ndim): die Punkte in ndim Dimensionen, aus denen das Voronoi-Diagramm generiert werden soll
radiusdouble: Radius der Sphäre
centerdouble Array der Form (ndim,): Mittelpunkt der Sphäre
verticesdouble Array der Form (nvertices, ndim): Voronoi-Vertices, die den Punkten entsprechen
regionsListe von Listen von ganzen Zahlen der Form (npoints, _ ): der n-te Eintrag ist eine Liste, die die Indizes der Vertices enthält, die zum n-ten Punkt in points gehören

Methoden

calculate_areas()

Berechnet die Flächen der Voronoi-Regionen.

Löst aus:

ValueError: Wenn Duplikate in points vorhanden sind. Wenn der bereitgestellte radius nicht mit points übereinstimmt.

Siehe auch

Voronoi: Konventionelle Voronoi-Diagramme in N Dimensionen.

Hinweise

Der Algorithmus für sphärische Voronoi-Diagramme geht wie folgt vor: Die konvexe Hülle der Eingabepunkte (Generatoren) wird berechnet und entspricht deren Delaunay-Triangulierung auf der Oberfläche der Sphäre [Caroli]. Die Nachbarschaftsinformation der konvexen Hülle wird dann verwendet, um die Vertices der Voronoi-Regionen um jeden Generator zu ordnen. Letzterer Ansatz ist wesentlich unempfindlicher gegenüber Gleitkommafehlern als winkelbasierte Methoden zur Sortierung der Voronoi-Region-Vertices.

Empirische Bewertung der Leistung des sphärischen Voronoi-Algorithmus deutet auf eine quadratische Zeitkomplexität hin (loglinear ist optimal, aber die Algorithmen sind schwieriger zu implementieren).

Referenzen

[Caroli]

Caroli et al. Robust and Efficient Delaunay triangulations of points on or close to a sphere. Research Report RR-7004, 2009.

[VanOosterom]

Van Oosterom and Strackee. The solid angle of a plane triangle. IEEE Transactions on Biomedical Engineering, 2, 1983, pp 125–126.

Beispiele

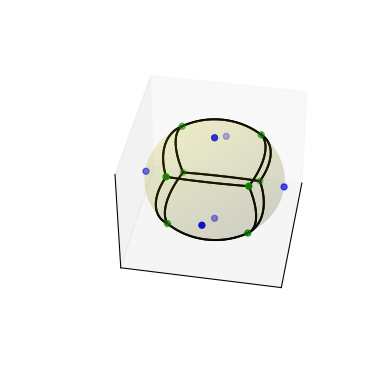
Einige Importe durchführen und Punkte auf einem Würfel nehmen

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.spatial import SphericalVoronoi, geometric_slerp
>>> from mpl_toolkits.mplot3d import proj3d
>>> # set input data
>>> points = np.array([[0, 0, 1], [0, 0, -1], [1, 0, 0],
...                    [0, 1, 0], [0, -1, 0], [-1, 0, 0], ])

Das sphärische Voronoi-Diagramm berechnen

>>> radius = 1
>>> center = np.array([0, 0, 0])
>>> sv = SphericalVoronoi(points, radius, center)

Plot generieren

>>> # sort vertices (optional, helpful for plotting)
>>> sv.sort_vertices_of_regions()
>>> t_vals = np.linspace(0, 1, 2000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')
>>> # plot the unit sphere for reference (optional)
>>> u = np.linspace(0, 2 * np.pi, 100)
>>> v = np.linspace(0, np.pi, 100)
>>> x = np.outer(np.cos(u), np.sin(v))
>>> y = np.outer(np.sin(u), np.sin(v))
>>> z = np.outer(np.ones(np.size(u)), np.cos(v))
>>> ax.plot_surface(x, y, z, color='y', alpha=0.1)
>>> # plot generator points
>>> ax.scatter(points[:, 0], points[:, 1], points[:, 2], c='b')
>>> # plot Voronoi vertices
>>> ax.scatter(sv.vertices[:, 0], sv.vertices[:, 1], sv.vertices[:, 2],
...                    c='g')
>>> # indicate Voronoi regions (as Euclidean polygons)
>>> for region in sv.regions:
...    n = len(region)
...    for i in range(n):
...        start = sv.vertices[region][i]
...        end = sv.vertices[region][(i + 1) % n]
...        result = geometric_slerp(start, end, t_vals)
...        ax.plot(result[..., 0],
...                result[..., 1],
...                result[..., 2],
...                c='k')
>>> ax.azim = 10
>>> ax.elev = 40
>>> _ = ax.set_xticks([])
>>> _ = ax.set_yticks([])
>>> _ = ax.set_zticks([])
>>> fig.set_size_inches(4, 4)
>>> plt.show()

../../_images/scipy-spatial-SphericalVoronoi-1.png