scipy.spatial.

geometric_slerp

scipy.spatial.geometric_slerp(start, end, t, tol=1e-07)

Geometrische sphärische lineare Interpolation.

Die Interpolation erfolgt entlang eines Bogens eines Großkreises mit Einheitsradius im Raum beliebiger Dimension.

Parameter:

start(n_dimensions, ) array-like

Einzelne n-dimensionale Eingabekoordinate in einem 1-D-Array-ähnlichen Objekt. n muss größer als 1 sein.

end(n_dimensions, ) array-like

Einzelne n-dimensionale Eingabekoordinate in einem 1-D-Array-ähnlichen Objekt. n muss größer als 1 sein.

tfloat oder (n_punkte, ) 1D array-like

Ein Float oder 1D-Array-ähnliches Objekt von Doubles, das Interpolationsparameter darstellt, wobei Werte im inklusiven Intervall zwischen 0 und 1 erforderlich sind. Ein gängiger Ansatz ist die Erzeugung des Arrays mit np.linspace(0, 1, n_pts) für linear verteilte Punkte. Aufsteigende, absteigende und gemischte Reihenfolgen sind zulässig.

tolfloat

Die absolute Toleranz für die Bestimmung, ob die Start- und Endkoordinaten Antipoden sind.

Rückgabe:

ergebnis(t.größe, D)

Ein Array von Doubles, das den interpolierten sphärischen Pfad enthält und Start und Ende einschließt, wenn 0 und 1 t verwendet werden. Die interpolierten Werte sollten der gleichen Sortierreihenfolge entsprechen, die im t-Array angegeben ist. Das Ergebnis kann eindimensional sein, wenn t ein Float ist.

Löst aus:

ValueError

Wenn start und end Antipoden sind, nicht auf der Einheits-n-Sphäre liegen oder bei einer Vielzahl von degenerierten Bedingungen.

Siehe auch

scipy.spatial.transform.Slerp

3-D Slerp, das mit Quaternionen arbeitet

Hinweise

Die Implementierung basiert auf der mathematischen Formel in [1], und die erste bekannte Darstellung dieses Algorithmus, abgeleitet aus dem Studium der 4-D-Geometrie, wird Glenn Davis in einer Fußnote der ursprünglichen Quaternionen-Slerp-Publikation von Ken Shoemake zugeschrieben [2].

Hinzugefügt in Version 1.5.0.

Referenzen

[1]

https://en.wikipedia.org/wiki/Slerp#Geometric_Slerp

[2]

Ken Shoemake (1985) Animating rotation with quaternion curves. ACM SIGGRAPH Computer Graphics, 19(3): 245-254.

Beispiele

Probieren Sie es in Ihrem Browser aus!

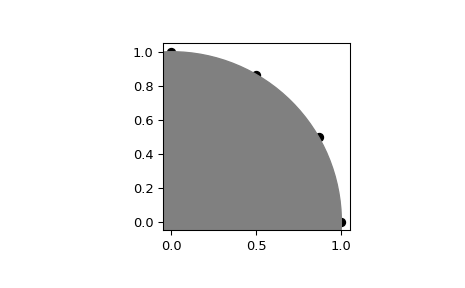
Interpoliere vier linear verteilte Werte auf dem Umfang eines Kreises, der 90 Grad überspannt

>>> import numpy as np
>>> from scipy.spatial import geometric_slerp
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> start = np.array([1, 0])
>>> end = np.array([0, 1])
>>> t_vals = np.linspace(0, 1, 4)
>>> result = geometric_slerp(start,
...                          end,
...                          t_vals)

Die interpolierten Ergebnisse sollten in 30-Grad-Intervallen auf dem Einheitskreis erkennbar sein

>>> ax.scatter(result[...,0], result[...,1], c='k')
>>> circle = plt.Circle((0, 0), 1, color='grey')
>>> ax.add_artist(circle)
>>> ax.set_aspect('equal')
>>> plt.show()

Der Versuch, zwischen Antipoden auf einem Kreis zu interpolieren, ist mehrdeutig, da es zwei mögliche Pfade gibt, und auf einer Sphäre gibt es unendlich viele mögliche Pfade auf der geodätischen Oberfläche. Nichtsdestotrotz wird einer der mehrdeutigen Pfade zusammen mit einer Warnung zurückgegeben.

>>> opposite_pole = np.array([-1, 0])
>>> with np.testing.suppress_warnings() as sup:
...     sup.filter(UserWarning)
...     geometric_slerp(start,
...                     opposite_pole,
...                     t_vals)
array([[ 1.00000000e+00,  0.00000000e+00],
       [ 5.00000000e-01,  8.66025404e-01],
       [-5.00000000e-01,  8.66025404e-01],
       [-1.00000000e+00,  1.22464680e-16]])

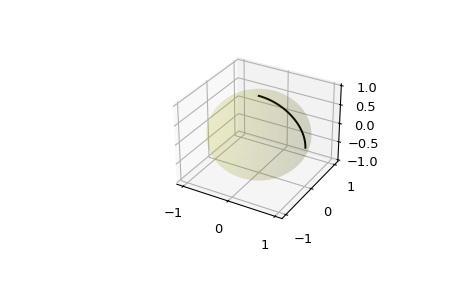
Erweitere das ursprüngliche Beispiel auf eine Sphäre und plote Interpolationspunkte in 3D

>>> from mpl_toolkits.mplot3d import proj3d
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')

Plote die Einheitskugel zur Referenz (optional)

>>> u = np.linspace(0, 2 * np.pi, 100)
>>> v = np.linspace(0, np.pi, 100)
>>> x = np.outer(np.cos(u), np.sin(v))
>>> y = np.outer(np.sin(u), np.sin(v))
>>> z = np.outer(np.ones(np.size(u)), np.cos(v))
>>> ax.plot_surface(x, y, z, color='y', alpha=0.1)

Die Interpolation über eine größere Anzahl von Punkten kann das Aussehen einer glatten Kurve auf der Oberfläche der Sphäre erzeugen, was auch für diskretisierte Integrationsberechnungen auf einer Sphärenoberfläche nützlich ist.

>>> start = np.array([1, 0, 0])
>>> end = np.array([0, 0, 1])
>>> t_vals = np.linspace(0, 1, 200)
>>> result = geometric_slerp(start,
...                          end,
...                          t_vals)
>>> ax.plot(result[...,0],
...         result[...,1],
...         result[...,2],
...         c='k')
>>> plt.show()

ZurückIn Tab öffnen