scipy.spatial.transform.

RotationSpline

class scipy.spatial.transform.RotationSpline(times, rotations)

Interpoliert Rotationen mit kontinuierlicher Winkelgeschwindigkeit und Beschleunigung.

Die Rotationsvektoren zwischen jeder aufeinanderfolgenden Ausrichtung sind kubische Funktionen der Zeit, und es ist garantiert, dass Winkelgeschwindigkeit und Beschleunigung kontinuierlich sind. Solche Interpolationen sind analog zur kubischen Spline-Interpolation.

Siehe [1] für mathematische und Implementierungsdetails.

Parameter:

timesarray_like, shape (N,)

Zeitpunkte der bekannten Rotationen. Es müssen mindestens 2 Zeitpunkte angegeben werden.

rotationsRotation Instanz

Rotationen, zwischen denen die Interpolation durchgeführt werden soll. Muss N Rotationen enthalten.

Methoden

__call__(times[, order])

Berechnet interpolierte Werte.

Referenzen

[1]

Glatte Lage-Interpolation

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> from scipy.spatial.transform import Rotation, RotationSpline
>>> import numpy as np

Definieren Sie die Sequenz von Zeiten und Rotationen aus den Euler-Winkeln

>>> times = [0, 10, 20, 40]
>>> angles = [[-10, 20, 30], [0, 15, 40], [-30, 45, 30], [20, 45, 90]]
>>> rotations = Rotation.from_euler('XYZ', angles, degrees=True)

Erstellen Sie das Interpolator-Objekt

>>> spline = RotationSpline(times, rotations)

Interpolieren Sie die Euler-Winkel, Winkelgeschwindigkeit und Beschleunigung

>>> angular_rate = np.rad2deg(spline(times, 1))
>>> angular_acceleration = np.rad2deg(spline(times, 2))
>>> times_plot = np.linspace(times[0], times[-1], 100)
>>> angles_plot = spline(times_plot).as_euler('XYZ', degrees=True)
>>> angular_rate_plot = np.rad2deg(spline(times_plot, 1))
>>> angular_acceleration_plot = np.rad2deg(spline(times_plot, 2))

Auf dieser Grafik sehen Sie, dass die Euler-Winkel kontinuierlich und glatt sind

>>> import matplotlib.pyplot as plt
>>> plt.plot(times_plot, angles_plot)
>>> plt.plot(times, angles, 'x')
>>> plt.title("Euler angles")
>>> plt.show()

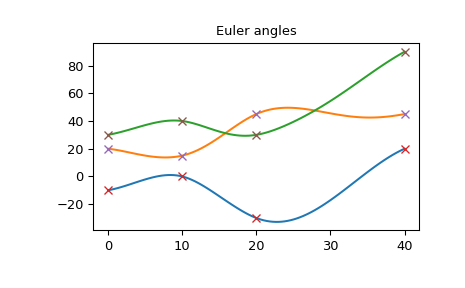
Die Winkelgeschwindigkeit ist ebenfalls glatt

>>> plt.plot(times_plot, angular_rate_plot)
>>> plt.plot(times, angular_rate, 'x')
>>> plt.title("Angular rate")
>>> plt.show()

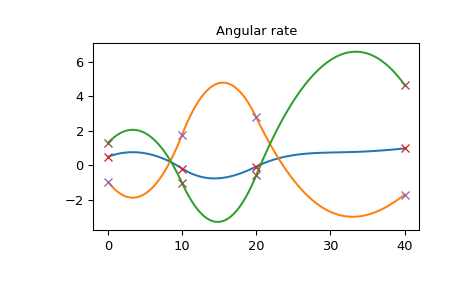
Die Winkelbeschleunigung ist kontinuierlich, aber nicht glatt. Beachten Sie auch, dass die Winkelbeschleunigung keine stückweise lineare Funktion ist, da sie sich von der zweiten Ableitung des Rotationsvektors unterscheidet (die, wie bei der kubischen Spline, eine stückweise lineare Funktion ist).

>>> plt.plot(times_plot, angular_acceleration_plot)
>>> plt.plot(times, angular_acceleration, 'x')
>>> plt.title("Angular acceleration")
>>> plt.show()

ZurückIn Tab öffnen