scipy.special.fdtr#

scipy.special.fdtr(dfn, dfd, x, out=None) = <ufunc 'fdtr'>#

F kumulative Verteilungsfunktion.

Gibt den Wert der kumulativen Verteilungsfunktion der F-Verteilung zurück, auch bekannt als Snedecors F-Verteilung oder Fisher-Snedecor-Verteilung.

Die F-Verteilung mit den Parametern \(d_n\) und \(d_d\) ist die Verteilung der Zufallsvariablen,

\[X = \frac{U_n/d_n}{U_d/d_d},\]

wobei \(U_n\) und \(U_d\) Zufallsvariablen sind, die \(\chi^2\)-verteilt sind, mit \(d_n\) bzw. \(d_d\) Freiheitsgraden.

Parameter:

dfnarray_like: Erster Parameter (positive Gleitkommazahl).
dfdarray_like: Zweiter Parameter (positive Gleitkommazahl).
xarray_like: Argument (nicht-negative Gleitkommazahl).
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

yskalar oder ndarray: Die CDF der F-Verteilung mit den Parametern dfn und dfd bei x.

Siehe auch

fdtrc: F-Verteilung Überlebensfunktion
fdtri: F-Verteilungs-Inverse kumulative Verteilung
scipy.stats.f: F-Verteilung

Hinweise

Die regularisierte unvollständige Betafunktion wird gemäß der Formel verwendet,

\[F(d_n, d_d; x) = I_{xd_n/(d_d + xd_n)}(d_n/2, d_d/2).\]

Wrapper für die Cephes-Routine [1] fdtr. Die F-Verteilung ist auch als scipy.stats.f verfügbar. Der direkte Aufruf von fdtr kann die Leistung im Vergleich zur cdf-Methode von scipy.stats.f verbessern (siehe letztes Beispiel unten).

Referenzen

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Beispiele

Berechnen Sie die Funktion für dfn=1 und dfd=2 bei x=1.

>>> import numpy as np
>>> from scipy.special import fdtr
>>> fdtr(1, 2, 1)
0.5773502691896258

Berechnen Sie die Funktion an mehreren Punkten, indem Sie ein NumPy-Array für x angeben.

>>> x = np.array([0.5, 2., 3.])
>>> fdtr(1, 2, x)
array([0.4472136 , 0.70710678, 0.77459667])

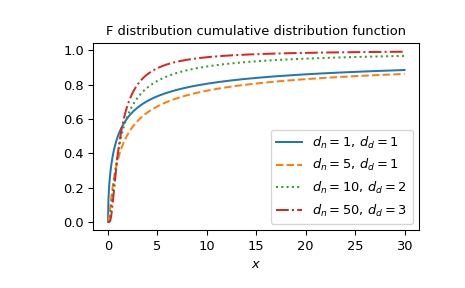
Plotten Sie die Funktion für mehrere Parametersätze.

>>> import matplotlib.pyplot as plt
>>> dfn_parameters = [1, 5, 10, 50]
>>> dfd_parameters = [1, 1, 2, 3]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(dfn_parameters, dfd_parameters,
...                            linestyles))
>>> x = np.linspace(0, 30, 1000)
>>> fig, ax = plt.subplots()
>>> for parameter_set in parameters_list:
...     dfn, dfd, style = parameter_set
...     fdtr_vals = fdtr(dfn, dfd, x)
...     ax.plot(x, fdtr_vals, label=rf"$d_n={dfn},\, d_d={dfd}$",
...             ls=style)
>>> ax.legend()
>>> ax.set_xlabel("$x$")
>>> ax.set_title("F distribution cumulative distribution function")
>>> plt.show()

../../_images/scipy-special-fdtr-1_00_00.png

Die F-Verteilung ist auch als scipy.stats.f verfügbar. Die direkte Verwendung von fdtr kann wesentlich schneller sein als der Aufruf der cdf-Methode von scipy.stats.f, insbesondere für kleine Arrays oder einzelne Werte. Um die gleichen Ergebnisse zu erzielen, muss die folgende Parametrisierung verwendet werden: stats.f(dfn, dfd).cdf(x)=fdtr(dfn, dfd, x).

>>> from scipy.stats import f
>>> dfn, dfd = 1, 2
>>> x = 1
>>> fdtr_res = fdtr(dfn, dfd, x)  # this will often be faster than below
>>> f_dist_res = f(dfn, dfd).cdf(x)
>>> fdtr_res == f_dist_res  # test that results are equal
True