scipy.special.gdtrc#

scipy.special.gdtrc(a, b, x, out=None) = <ufunc 'gdtrc'>#

Überlebensfunktion der Gammaverteilung.

Integral von x bis unendlich der Gamma-Wahrscheinlichkeitsdichtefunktion,

\[F = \int_x^\infty \frac{a^b}{\Gamma(b)} t^{b-1} e^{-at}\,dt,\]

wobei \(\Gamma\) die Gamma-Funktion ist.

Parameter:

aarray_like: Der Ratenparameter der Gammaverteilung, manchmal bezeichnet als \(\beta\) (float). Er ist auch der Kehrwert des Skalenparameters \(\theta\).
barray_like: Der Formparameter der Gammaverteilung, manchmal bezeichnet als \(\alpha\) (float).
xarray_like: Das Quantil (untere Integrationsgrenze; float).
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

FSkalar oder ndarray: Die Überlebensfunktion der Gammaverteilung mit den Parametern a und b, ausgewertet an der Stelle x.

Siehe auch

gdtr: Kumulative Verteilungsfunktion der Gammaverteilung
scipy.stats.gamma: Gamma-Verteilung
gdtrix

Hinweise

Die Auswertung erfolgt unter Verwendung des Zusammenhangs zur unvollständigen Gammafunktion (regularisierte Gammafunktion).

Wrapper für die Cephes-Routine [1] gdtrc. Das direkte Aufrufen von gdtrc kann die Leistung im Vergleich zur sf-Methode von scipy.stats.gamma verbessern (siehe letztes Beispiel unten).

Referenzen

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Beispiele

Berechnen Sie die Funktion für a=1 und b=2 an der Stelle x=5.

>>> import numpy as np
>>> from scipy.special import gdtrc
>>> import matplotlib.pyplot as plt
>>> gdtrc(1., 2., 5.)
0.04042768199451279

Berechnen Sie die Funktion für a=1, b=2 an mehreren Stellen, indem Sie ein NumPy-Array für x bereitstellen.

>>> xvalues = np.array([1., 2., 3., 4])
>>> gdtrc(1., 1., xvalues)
array([0.36787944, 0.13533528, 0.04978707, 0.01831564])

gdtrc kann verschiedene Parametersätze auswerten, indem Arrays mit Broadcasting-kompatiblen Formen für a, b und x bereitgestellt werden. Hier berechnen wir die Funktion für drei verschiedene a an vier Positionen x und b=3, was zu einem 3x4-Array führt.

>>> a = np.array([[0.5], [1.5], [2.5]])
>>> x = np.array([1., 2., 3., 4])
>>> a.shape, x.shape
((3, 1), (4,))

>>> gdtrc(a, 3., x)
array([[0.98561232, 0.9196986 , 0.80884683, 0.67667642],
       [0.80884683, 0.42319008, 0.17357807, 0.0619688 ],
       [0.54381312, 0.12465202, 0.02025672, 0.0027694 ]])

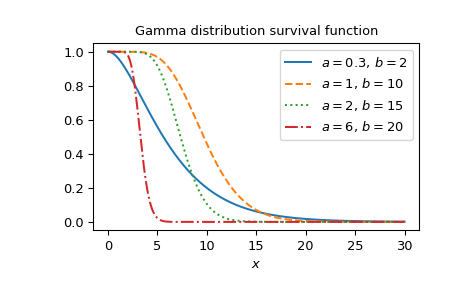
Plotten der Funktion für vier verschiedene Parametersätze.

>>> a_parameters = [0.3, 1, 2, 6]
>>> b_parameters = [2, 10, 15, 20]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(a_parameters, b_parameters, linestyles))
>>> x = np.linspace(0, 30, 1000)
>>> fig, ax = plt.subplots()
>>> for parameter_set in parameters_list:
...     a, b, style = parameter_set
...     gdtrc_vals = gdtrc(a, b, x)
...     ax.plot(x, gdtrc_vals, label=fr"$a= {a},\, b={b}$", ls=style)
>>> ax.legend()
>>> ax.set_xlabel("$x$")
>>> ax.set_title("Gamma distribution survival function")
>>> plt.show()

../../_images/scipy-special-gdtrc-1_00_00.png

Die Gammaverteilung ist auch als scipy.stats.gamma verfügbar. Die direkte Verwendung von gdtrc kann wesentlich schneller sein als das Aufrufen der sf-Methode von scipy.stats.gamma, insbesondere für kleine Arrays oder einzelne Werte. Um die gleichen Ergebnisse zu erhalten, muss die folgende Parametrisierung verwendet werden: stats.gamma(b, scale=1/a).sf(x)=gdtrc(a, b, x).

>>> from scipy.stats import gamma
>>> a = 2
>>> b = 3
>>> x = 1.
>>> gdtrc_result = gdtrc(a, b, x)  # this will often be faster than below
>>> gamma_dist_result = gamma(b, scale=1/a).sf(x)
>>> gdtrc_result == gamma_dist_result  # test that results are equal
True