scipy.special.i1e#

scipy.special.i1e(x, out=None) = <ufunc 'i1e'>#

Exponentiell skalierte modifizierte Besselfunktion der Ordnung 1.

Definiert als

i1e(x) = exp(-abs(x)) * i1(x)

Parameter:

xarray_like: Argument (float)
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

ISkalar oder ndarray: Wert der exponentiell skalierten modifizierten Besselfunktion der Ordnung 1 bei x.

Siehe auch

iv: Modifizierte Besselfunktion erster Art
i1: Modifizierte Besselfunktion der Ordnung 1

Hinweise

Der Bereich wird in die zwei Intervalle [0, 8] und (8, Unendlich) aufgeteilt. Chebyshev-Polynom-Entwicklungen werden in jedem Intervall verwendet. Die verwendeten Polynom-Entwicklungen sind die gleichen wie bei i1, sie werden jedoch nicht mit dem dominanten exponentiellen Faktor multipliziert.

Diese Funktion ist ein Wrapper für die Cephes [1] Routine i1e. i1e ist nützlich für große Argumente x: für diese läuft i1 schnell über.

i1e bietet experimentelle Unterstützung für Backends, die mit dem Python Array API Standard kompatibel sind, zusätzlich zu NumPy. Bitte erwägen Sie, diese Funktionen zu testen, indem Sie die Umgebungsvariable SCIPY_ARRAY_API=1 setzen und CuPy-, PyTorch-, JAX- oder Dask-Arrays als Array-Argumente bereitstellen. Die folgenden Kombinationen von Backend und Gerät (oder anderer Funktionalität) werden unterstützt.

Bibliothek	CPU	GPU
NumPy	✅	n/a
CuPy	n/a	✅
PyTorch	✅	✅
JAX	✅	✅
Dask	✅	n/a

Siehe Unterstützung für den Array API Standard für weitere Informationen.

Referenzen

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Beispiele

Im folgenden Beispiel gibt i1 Unendlichkeit zurück, während i1e immer noch eine endliche Zahl zurückgibt.

>>> from scipy.special import i1, i1e
>>> i1(1000.), i1e(1000.)
(inf, 0.01261093025692863)

Berechnen Sie die Funktion an mehreren Punkten, indem Sie ein NumPy-Array oder eine Liste für x angeben.

>>> import numpy as np
>>> i1e(np.array([-2., 0., 6.]))
array([-0.21526929,  0.        ,  0.15205146])

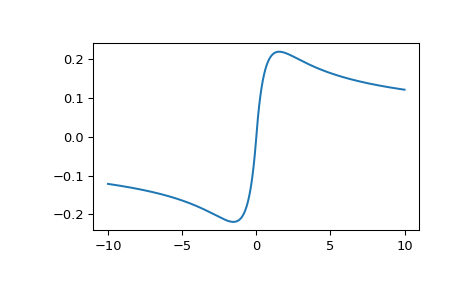
Plotten der Funktion zwischen -10 und 10.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(-10., 10., 1000)
>>> y = i1e(x)
>>> ax.plot(x, y)
>>> plt.show()