scipy.special.pseudo_huber

scipy.special.pseudo_huber(delta, r, out=None) = <ufunc 'pseudo_huber'>

Pseudo-Huber-Verlustfunktion.

\[\mathrm{pseudo\_huber}(\delta, r) = \delta^2 \left( \sqrt{ 1 + \left( \frac{r}{\delta} \right)^2 } - 1 \right)\]

Parameter:

deltaarray_like

Eingabearray, das den Umschaltpunkt für den weichen quadratischen vs. linearen Verlust angibt.

rarray_like

Eingabearray, das möglicherweise Residuen darstellt.

outndarray, optional

Optionales Ausgabe-Array für die Funktionsergebnisse

Rückgabe:

resSkalar oder ndarray

Die berechneten Werte der Pseudo-Huber-Verlustfunktion.

Siehe auch

huber

Ähnliche Funktion, die diese Funktion annähert

Hinweise

Ähnlich wie huber dient pseudo_huber oft als robuste Verlustfunktion in der Statistik oder im maschinellen Lernen, um den Einfluss von Ausreißern zu reduzieren. Im Gegensatz zu huber ist pseudo_huber glatt.

Typischerweise repräsentiert r Residuen, die Differenz zwischen einer Modellvorhersage und den Daten. Dann, für \(|r|\leq\delta\), ähnelt pseudo_huber dem quadrierten Fehler und für \(|r|>\delta\) dem absoluten Fehler. Auf diese Weise erzielt die Pseudo-Huber-Verlustfunktion oft eine schnelle Konvergenz bei der Modellanpassung für kleine Residuen, ähnlich der quadratischen Fehlerverlustfunktion, und reduziert dennoch den Einfluss von Ausreißern (\(|r|>\delta\)) wie die absolute Fehlerverlustfunktion. Da \(\delta\) der Grenzwert zwischen den Regimen des quadratischen und absoluten Fehlers ist, muss er sorgfältig für jedes Problem abgestimmt werden. pseudo_huber ist außerdem konvex, was sie für gradientenbasierte Optimierungen geeignet macht. [1] [2]

Hinzugefügt in Version 0.15.0.

Referenzen

[1]

Hartley, Zisserman, “Multiple View Geometry in Computer Vision”. 2003. Cambridge University Press. S. 619

[2]

Charbonnier et al. „Deterministic edge-preserving regularization in computed imaging“. 1997. IEEE Trans. Image Processing. 6 (2): 298 - 311.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Importieren Sie alle notwendigen Module.

>>> import numpy as np
>>> from scipy.special import pseudo_huber, huber
>>> import matplotlib.pyplot as plt

Berechnen Sie die Funktion für delta=1 bei r=2.

>>> pseudo_huber(1., 2.)
1.2360679774997898

Berechnen Sie die Funktion bei r=2 für verschiedene delta, indem Sie eine Liste oder ein NumPy-Array für delta bereitstellen.

>>> pseudo_huber([1., 2., 4.], 3.)
array([2.16227766, 3.21110255, 4.        ])

Berechnen Sie die Funktion für delta=1 an mehreren Punkten, indem Sie eine Liste oder ein NumPy-Array für r bereitstellen.

>>> pseudo_huber(2., np.array([1., 1.5, 3., 4.]))
array([0.47213595, 1.        , 3.21110255, 4.94427191])

Die Funktion kann für verschiedene delta und r berechnet werden, indem Arrays für beide mit kompatiblen Formen für Broadcasting bereitgestellt werden.

>>> r = np.array([1., 2.5, 8., 10.])
>>> deltas = np.array([[1.], [5.], [9.]])
>>> print(r.shape, deltas.shape)
(4,) (3, 1)

>>> pseudo_huber(deltas, r)
array([[ 0.41421356,  1.6925824 ,  7.06225775,  9.04987562],
       [ 0.49509757,  2.95084972, 22.16990566, 30.90169944],
       [ 0.49846624,  3.06693762, 27.37435121, 40.08261642]])

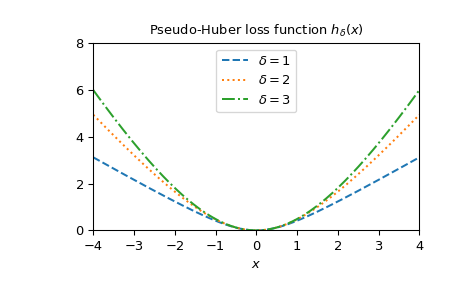
Zeichnen Sie die Funktion für verschiedene delta auf.

>>> x = np.linspace(-4, 4, 500)
>>> deltas = [1, 2, 3]
>>> linestyles = ["dashed", "dotted", "dashdot"]
>>> fig, ax = plt.subplots()
>>> combined_plot_parameters = list(zip(deltas, linestyles))
>>> for delta, style in combined_plot_parameters:
...     ax.plot(x, pseudo_huber(delta, x), label=rf"$\delta={delta}$",
...             ls=style)
>>> ax.legend(loc="upper center")
>>> ax.set_xlabel("$x$")
>>> ax.set_title(r"Pseudo-Huber loss function $h_{\delta}(x)$")
>>> ax.set_xlim(-4, 4)
>>> ax.set_ylim(0, 8)
>>> plt.show()

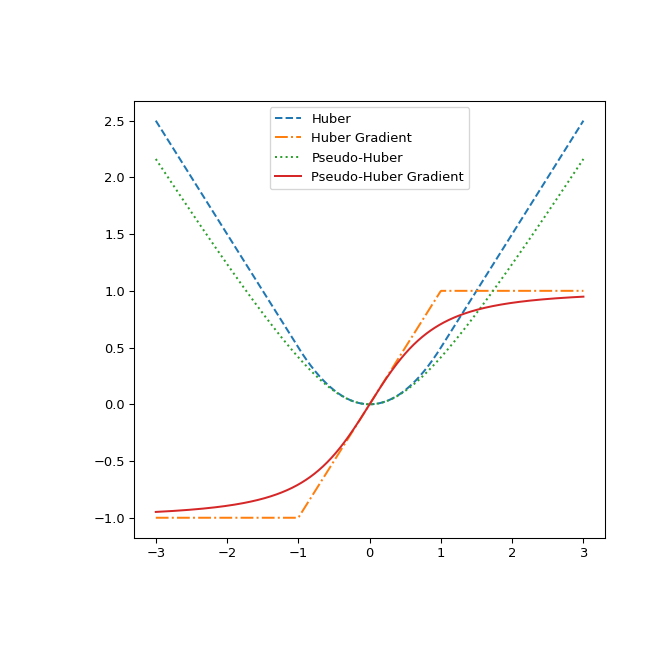
Schließlich veranschaulichen wir den Unterschied zwischen huber und pseudo_huber, indem wir sie und ihre Ableitungen nach r darstellen. Die Grafik zeigt, dass pseudo_huber stetig differenzierbar ist, während huber an den Punkten \(\pm\delta\) nicht stetig differenzierbar ist.

>>> def huber_grad(delta, x):
...     grad = np.copy(x)
...     linear_area = np.argwhere(np.abs(x) > delta)
...     grad[linear_area]=delta*np.sign(x[linear_area])
...     return grad
>>> def pseudo_huber_grad(delta, x):
...     return x* (1+(x/delta)**2)**(-0.5)
>>> x=np.linspace(-3, 3, 500)
>>> delta = 1.
>>> fig, ax = plt.subplots(figsize=(7, 7))
>>> ax.plot(x, huber(delta, x), label="Huber", ls="dashed")
>>> ax.plot(x, huber_grad(delta, x), label="Huber Gradient", ls="dashdot")
>>> ax.plot(x, pseudo_huber(delta, x), label="Pseudo-Huber", ls="dotted")
>>> ax.plot(x, pseudo_huber_grad(delta, x), label="Pseudo-Huber Gradient",
...         ls="solid")
>>> ax.legend(loc="upper center")
>>> plt.show()

ZurückIn Tab öffnen