scipy.special.

y1_zeros

scipy.special.y1_zeros(nt, complex=False)

Berechnet nt Nullstellen der Bessel-Funktion Y1(z) und die Ableitung an jeder Nullstelle.

Die Ableitungen sind gegeben durch Y1’(z1) = Y0(z1) an jeder Nullstelle z1.

Parameter:

ntint

Anzahl der zurückzugebenden Nullstellen

complexbool, Standardwert False

Setzen Sie auf False, um nur die reellen Nullstellen zurückzugeben; setzen Sie auf True, um nur die komplexen Nullstellen mit negativem Realteil und positivem Imaginärteil zurückzugeben. Beachten Sie, dass die komplexen Konjugierten der letzteren ebenfalls Nullstellen der Funktion sind, aber von dieser Routine nicht zurückgegeben werden.

Rückgabe:

z1nndarray

Position der n-ten Nullstelle von Y1(z)

y1pz1nndarray

Wert der Ableitung Y1’(z1) für die n-te Nullstelle

Referenzen

[1]

Zhang, Shanjie und Jin, Jianming. „Computation of Special Functions“, John Wiley and Sons, 1996, Kapitel 5. https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html

Beispiele

Probieren Sie es in Ihrem Browser aus!

Berechnen Sie die ersten 4 reellen Wurzeln und die Ableitungen an den Wurzeln von \(Y_1\)

>>> import numpy as np
>>> from scipy.special import y1_zeros
>>> zeros, grads = y1_zeros(4)
>>> with np.printoptions(precision=5):
...     print(f"Roots: {zeros}")
...     print(f"Gradients: {grads}")
Roots: [ 2.19714+0.j  5.42968+0.j  8.59601+0.j 11.74915+0.j]
Gradients: [ 0.52079+0.j -0.34032+0.j  0.27146+0.j -0.23246+0.j]

Extrahieren Sie die Realteile

>>> realzeros = zeros.real
>>> realzeros
array([ 2.19714133,  5.42968104,  8.59600587, 11.74915483])

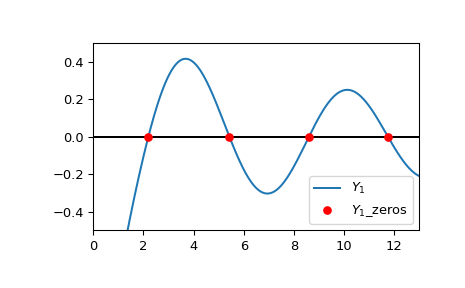
Plotten Sie \(Y_1\) und die ersten vier berechneten Wurzeln.

>>> import matplotlib.pyplot as plt
>>> from scipy.special import y1
>>> xmin = 0
>>> xmax = 13
>>> x = np.linspace(xmin, xmax, 500)
>>> zeros, grads = y1_zeros(4)
>>> fig, ax = plt.subplots()
>>> ax.hlines(0, xmin, xmax, color='k')
>>> ax.plot(x, y1(x), label=r'$Y_1$')
>>> ax.scatter(zeros.real, np.zeros((4, )), s=30, c='r',
...            label=r'$Y_1$_zeros', zorder=5)
>>> ax.set_ylim(-0.5, 0.5)
>>> ax.set_xlim(xmin, xmax)
>>> plt.legend()
>>> plt.show()

Berechnen Sie die ersten 4 komplexen Wurzeln und die Ableitungen an den Wurzeln von \(Y_1\), indem Sie complex=True setzen

>>> y1_zeros(4, True)
(array([ -0.50274327+0.78624371j,  -3.83353519+0.56235654j,
         -7.01590368+0.55339305j, -10.17357383+0.55127339j]),
 array([-0.45952768+1.31710194j,  0.04830191-0.69251288j,
        -0.02012695+0.51864253j,  0.011614  -0.43203296j]))

ZurückIn Tab öffnen