scipy.stats.Normal.

plot#

Normal.plot(x='x', y=None, *, t=None, ax=None)[Quelle]#

Zeichnet eine Funktion der Verteilung.

Hilfsfunktion zur schnellen Visualisierung der der Zufallsvariable zugrunde liegenden Verteilung.

Parameter:

x, ystr, optional: Zeichenkette, die die für Abszisse und Ordinate (horizontale und vertikale Koordinaten) zu verwendenden Größen angibt. Standardwerte sind 'x' (die Domäne der Zufallsvariable) und entweder 'pdf' (die Wahrscheinlichkeitsdichtefunktion) (stetig) oder 'pdf' (die Wahrscheinlichkeitsdichtefunktion) (diskret). Gültige Werte sind: ‘x’, ‘pdf’, ‘pmf’, ‘cdf’, ‘ccdf’, ‘icdf’, ‘iccdf’, ‘logpdf’, ‘logpmf’, ‘logcdf’, ‘logccdf’, ‘ilogcdf’, ‘ilogccdf’.
t3-Tupel aus (str, float, float), optional: Tupel, das die Grenzen angibt, innerhalb derer die Größen geplottet werden. Der Standardwert ist ('cdf', 0.0005, 0.9995), wenn die Domäne unendlich ist, was bedeutet, dass die zentralen 99,9 % der Verteilung angezeigt werden sollen; andernfalls werden die Endpunkte des Trägers verwendet, sofern diese endlich sind. Gültige Werte sind: ‘x’, ‘cdf’, ‘ccdf’, ‘icdf’, ‘iccdf’, ‘logcdf’, ‘logccdf’, ‘ilogcdf’, ‘ilogccdf’.
axmatplotlib.axes, optional: Achsen, auf denen der Plot generiert werden soll. Wenn nicht angegeben, werden die aktuellen Achsen verwendet.

Rückgabe:

axmatplotlib.axes: Achsen, auf denen der Plot generiert wurde. Der Plot kann durch Manipulation dieses Objekts angepasst werden.

Beispiele

Instanziieren Sie eine Verteilung mit den gewünschten Parametern

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> X = stats.Normal(mu=1., sigma=2.)

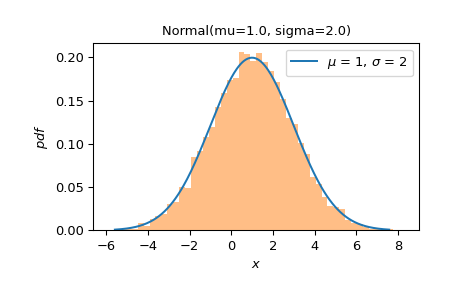
Plottet die PDF über die zentralen 99,9 % der Verteilung. Vergleicht dies mit einem Histogramm einer Zufallsstichprobe.

>>> ax = X.plot()
>>> sample = X.sample(10000)
>>> ax.hist(sample, density=True, bins=50, alpha=0.5)
>>> plt.show()

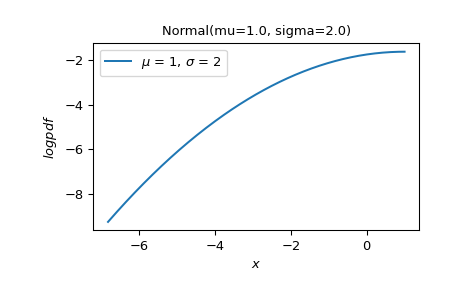
Plottet logpdf(x) als Funktion von x im linken Schwanz, wobei der Logarithmus der CDF zwischen -10 und np.log(0.5) liegt.

>>> X.plot('x', 'logpdf', t=('logcdf', -10, np.log(0.5)))
>>> plt.show()

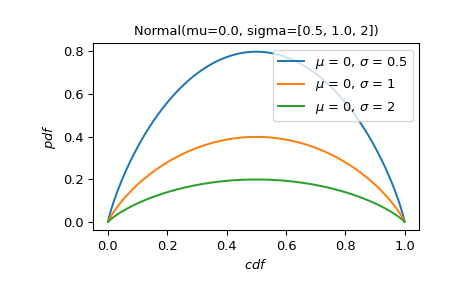
Plottet die PDF der Normalverteilung als Funktion der CDF für verschiedene Werte des Skalierungsparameters.

>>> X = stats.Normal(mu=0., sigma=[0.5, 1., 2])
>>> X.plot('cdf', 'pdf')
>>> plt.show()