bayes_mvs#
- scipy.stats.bayes_mvs(data, alpha=0.9)[Quelle]#
Bayesian-Konfidenzintervalle für Mittelwert, Varianz und Standardabweichung.
- Parameter:
- dataarray_like
Eingabedaten, wenn mehrdimensional, werden von
bayes_mvsauf 1-D abgeflacht. Erfordert 2 oder mehr Datenpunkte.- alphafloat, optional
Wahrscheinlichkeit, dass das zurückgegebene Konfidenzintervall den wahren Parameter enthält.
- Rückgabe:
- mean_cntr, var_cntr, std_cntrTupel
Die drei Ergebnisse beziehen sich jeweils auf den Mittelwert, die Varianz und die Standardabweichung. Jedes Ergebnis ist ein Tupel der Form
(center, (lower, upper))
mit
centerdem Mittelwert der bedingten Wahrscheinlichkeitsdichtefunktion des Wertes gegeben die Daten, und(lower, upper)ein Konfidenzintervall, zentriert um den Median, das die Schätzung mit einer Wahrscheinlichkeit vonalphaenthält.
Siehe auch
Hinweise
Jedes Tupel von Schätzungen für Mittelwert, Varianz und Standardabweichung repräsentiert (center, (lower, upper)) wobei center der Mittelwert der bedingten Wahrscheinlichkeitsdichtefunktion des Wertes gegeben die Daten ist und (lower, upper) ein Konfidenzintervall ist, das zentriert um den Median ist und die Schätzung mit einer Wahrscheinlichkeit von
alphaenthält.Konvertiert Daten in 1-D und geht davon aus, dass alle Daten den gleichen Mittelwert und die gleiche Varianz haben. Verwendet Jeffrey's Prior für Varianz und Standardabweichung.
Äquivalent zu
tuple((x.mean(), x.interval(alpha)) for x in mvsdist(dat))Referenzen
T.E. Oliphant, „A Bayesian perspective on estimating mean, variance, and standard-deviation from data“, https://scholarsarchive.byu.edu/facpub/278, 2006.
Beispiele
Zuerst ein einfaches Beispiel, um die Ausgaben zu demonstrieren
>>> from scipy import stats >>> data = [6, 9, 12, 7, 8, 8, 13] >>> mean, var, std = stats.bayes_mvs(data) >>> mean Mean(statistic=9.0, minmax=(7.103650222612533, 10.896349777387467)) >>> var Variance(statistic=10.0, minmax=(3.176724206, 24.45910382)) >>> std Std_dev(statistic=2.9724954732045084, minmax=(1.7823367265645143, 4.945614605014631))
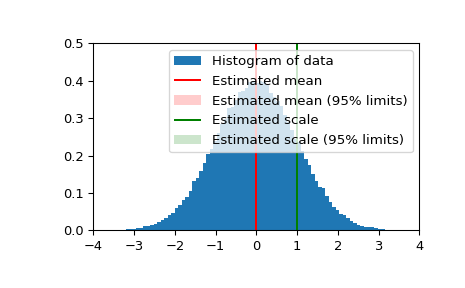
Nun generieren wir normalverteilte Zufallsdaten und erhalten Schätzungen für Mittelwert und Standardabweichung mit 95% Konfidenzintervallen für diese Schätzungen
>>> n_samples = 100000 >>> data = stats.norm.rvs(size=n_samples) >>> res_mean, res_var, res_std = stats.bayes_mvs(data, alpha=0.95)
>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> ax.hist(data, bins=100, density=True, label='Histogram of data') >>> ax.vlines(res_mean.statistic, 0, 0.5, colors='r', label='Estimated mean') >>> ax.axvspan(res_mean.minmax[0],res_mean.minmax[1], facecolor='r', ... alpha=0.2, label=r'Estimated mean (95% limits)') >>> ax.vlines(res_std.statistic, 0, 0.5, colors='g', label='Estimated scale') >>> ax.axvspan(res_std.minmax[0],res_std.minmax[1], facecolor='g', alpha=0.2, ... label=r'Estimated scale (95% limits)')
>>> ax.legend(fontsize=10) >>> ax.set_xlim([-4, 4]) >>> ax.set_ylim([0, 0.5]) >>> plt.show()