scipy.stats.

binned_statistic

scipy.stats.binned_statistic(x, values, statistic='mean', bins=10, range=None)

Berechnet eine gebinnte Statistik für einen oder mehrere Datensätze.

Dies ist eine Verallgemeinerung einer Histogrammfunktion. Ein Histogramm teilt den Raum in Bins auf und gibt die Anzahl der Punkte in jedem Bin zurück. Diese Funktion ermöglicht die Berechnung der Summe, des Mittelwerts, des Medians oder anderer Statistiken der Werte (oder einer Menge von Werten) innerhalb jedes Bins.

Parameter:

x(N,) array_like

Eine Sequenz von Werten, die gebinnt werden sollen.

values(N,) array_like oder Liste von (N,) array_like

Die Daten, auf denen die Statistik berechnet wird. Dies muss die gleiche Form wie x haben, oder eine Menge von Sequenzen – jede mit der gleichen Form wie x. Wenn values eine Menge von Sequenzen ist, wird die Statistik für jede unabhängig berechnet.

statisticstring oder callable, optional

Die zu berechnende Statistik (Standard ist 'mean'). Die folgenden Statistiken sind verfügbar

• ‘mean’ : berechnet den Mittelwert der Werte für Punkte innerhalb jedes Bins. Leere Bins werden durch NaN dargestellt.

• ‘std’ : Berechnung der Standardabweichung innerhalb jedes Bins. Dies wird implizit mit ddof=0 berechnet.

• ‘median’ : berechnet den Median der Werte für Punkte innerhalb jedes Bins. Leere Bins werden durch NaN dargestellt.

• ‘count’ : berechnet die Anzahl der Punkte innerhalb jedes Bins. Dies ist identisch mit einem ungewichteten Histogramm. Das values-Array wird nicht referenziert.

• ‘sum’ : berechnet die Summe der Werte für Punkte innerhalb jedes Bins. Dies ist identisch mit einem gewichteten Histogramm.

• ‘min’ : berechnet das Minimum der Werte für Punkte innerhalb jedes Bins. Leere Bins werden durch NaN dargestellt.

• ‘max’ : berechnet das Maximum der Werte für Punkte innerhalb jedes Bins. Leere Bins werden durch NaN dargestellt.

• function : eine benutzerdefinierte Funktion, die ein 1D-Array von Werten entgegennimmt und eine einzelne numerische Statistik zurückgibt. Diese Funktion wird für die Werte in jedem Bin aufgerufen. Leere Bins werden durch function([]) dargestellt, oder durch NaN, wenn diese einen Fehler zurückgibt.

binsint oder Sequenz von Skalaren, optional

Wenn bins ein Integer ist, definiert es die Anzahl gleicher Bins in dem angegebenen Bereich (Standard ist 10). Wenn bins eine Sequenz ist, definiert es die Bin-Ränder, einschließlich des rechtesten Rands, was nicht-uniforme Bin-Breiten ermöglicht. Werte in x, die kleiner als der niedrigste Bin-Rand sind, werden dem Bin 0 zugeordnet, Werte jenseits des höchsten Bins werden bins[-1] zugeordnet. Wenn die Bin-Ränder angegeben sind, beträgt die Anzahl der Bins (nx = len(bins)-1).

range(float, float) oder [(float, float)], optional

Der untere und obere Bereich der Bins. Wenn nicht angegeben, ist der Bereich einfach (x.min(), x.max()). Werte außerhalb des Bereichs werden ignoriert.

Rückgabe:

statisticarray

Die Werte der ausgewählten Statistik in jedem Bin.

bin_edgesArray vom Datentyp float

Gibt die Bin-Ränder zurück (Länge(statistic)+1).

binnumber: 1-D ndarray von Integers

Indizes der Bins (entsprechend bin_edges), zu denen jeder Wert von x gehört. Gleiche Länge wie values. Eine binnumber von i bedeutet, dass der entsprechende Wert zwischen (bin_edges[i-1], bin_edges[i]) liegt.

Siehe auch

numpy.digitize, numpy.histogram, binned_statistic_2d, binned_statistic_dd

Hinweise

Alle außer dem letzten (rechtesten) Bin sind halboffen. Mit anderen Worten, wenn bins [1, 2, 3, 4] ist, dann ist das erste Bin [1, 2) (inklusive 1, aber exklusive 2) und das zweite [2, 3). Das letzte Bin ist jedoch [3, 4], welches 4 *inklusive* enthält.

Hinzugefügt in Version 0.11.0.

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt

Zuerst einige grundlegende Beispiele

Erstellt zwei gleichmäßig verteilte Bins im Bereich der gegebenen Stichprobe und summiert die entsprechenden Werte in jedem dieser Bins.

>>> values = [1.0, 1.0, 2.0, 1.5, 3.0]
>>> stats.binned_statistic([1, 1, 2, 5, 7], values, 'sum', bins=2)
BinnedStatisticResult(statistic=array([4. , 4.5]),
        bin_edges=array([1., 4., 7.]), binnumber=array([1, 1, 1, 2, 2]))

Mehrere Arrays von Werten können ebenfalls übergeben werden. Die Statistik wird für jeden Satz unabhängig berechnet.

>>> values = [[1.0, 1.0, 2.0, 1.5, 3.0], [2.0, 2.0, 4.0, 3.0, 6.0]]
>>> stats.binned_statistic([1, 1, 2, 5, 7], values, 'sum', bins=2)
BinnedStatisticResult(statistic=array([[4. , 4.5],
       [8. , 9. ]]), bin_edges=array([1., 4., 7.]),
       binnumber=array([1, 1, 1, 2, 2]))

>>> stats.binned_statistic([1, 2, 1, 2, 4], np.arange(5), statistic='mean',
...                        bins=3)
BinnedStatisticResult(statistic=array([1., 2., 4.]),
        bin_edges=array([1., 2., 3., 4.]),
        binnumber=array([1, 2, 1, 2, 3]))

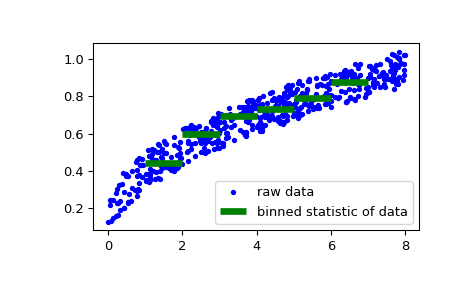
Als zweites Beispiel generieren wir nun einige Zufallsdaten zur Segelbootgeschwindigkeit in Abhängigkeit von der Windgeschwindigkeit und ermitteln dann, wie schnell unser Boot bei bestimmten Windgeschwindigkeiten ist.

>>> rng = np.random.default_rng()
>>> windspeed = 8 * rng.random(500)
>>> boatspeed = .3 * windspeed**.5 + .2 * rng.random(500)
>>> bin_means, bin_edges, binnumber = stats.binned_statistic(windspeed,
...                 boatspeed, statistic='median', bins=[1,2,3,4,5,6,7])
>>> plt.figure()
>>> plt.plot(windspeed, boatspeed, 'b.', label='raw data')
>>> plt.hlines(bin_means, bin_edges[:-1], bin_edges[1:], colors='g', lw=5,
...            label='binned statistic of data')
>>> plt.legend()

Nun können wir binnumber verwenden, um alle Datenpunkte mit einer Windgeschwindigkeit unter 1 auszuwählen.

>>> low_boatspeed = boatspeed[binnumber == 0]

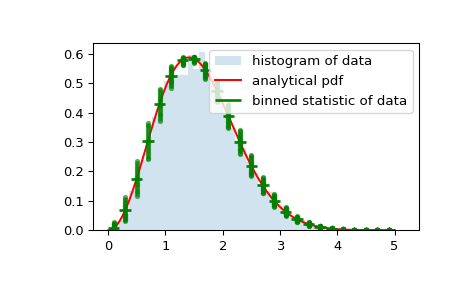
Als letztes Beispiel verwenden wir bin_edges und binnumber, um eine Verteilung zu plotten, die den Mittelwert und die Streuung um diesen Mittelwert pro Bin anzeigt, überlagert mit einem regulären Histogramm und der Wahrscheinlichkeitsdichtefunktion.

>>> x = np.linspace(0, 5, num=500)
>>> x_pdf = stats.maxwell.pdf(x)
>>> samples = stats.maxwell.rvs(size=10000)

>>> bin_means, bin_edges, binnumber = stats.binned_statistic(x, x_pdf,
...         statistic='mean', bins=25)
>>> bin_width = (bin_edges[1] - bin_edges[0])
>>> bin_centers = bin_edges[1:] - bin_width/2

>>> plt.figure()
>>> plt.hist(samples, bins=50, density=True, histtype='stepfilled',
...          alpha=0.2, label='histogram of data')
>>> plt.plot(x, x_pdf, 'r-', label='analytical pdf')
>>> plt.hlines(bin_means, bin_edges[:-1], bin_edges[1:], colors='g', lw=2,
...            label='binned statistic of data')
>>> plt.plot((binnumber - 0.5) * bin_width, x_pdf, 'g.', alpha=0.5)
>>> plt.legend(fontsize=10)
>>> plt.show()

ZurückIn Tab öffnen