scipy.stats.

differential_entropy

scipy.stats.differential_entropy(values, *, window_length=None, base=None, axis=0, method='auto', nan_policy='propagate', keepdims=False)

Schätzt die differentielle Entropie aus einer Stichprobe einer Verteilung.

Mehrere Schätzmethoden sind über den Parameter method verfügbar. Standardmäßig wird eine Methode basierend auf der Größe der Stichprobe ausgewählt.

Parameter:

valuesSequenz

Stichprobe aus einer kontinuierlichen Verteilung.

window_lengthint, optional

Fensterlänge für die Berechnung der Vasicek-Schätzung. Muss eine ganze Zahl zwischen 1 und der Hälfte der Stichprobengröße sein. Wenn None (Standardwert), wird der heuristische Wert verwendet

\[\left \lfloor \sqrt{n} + 0.5 \right \rfloor\]

wobei \(n\) die Stichprobengröße ist. Diese Heuristik wurde ursprünglich in [2] vorgeschlagen und ist in der Literatur üblich geworden.

basefloat, optional

Die zu verwendende logarithmische Basis, Standardwert ist e (natürlicher Logarithmus).

axisint oder None, Standard: 0

Wenn es sich um eine ganze Zahl handelt, ist dies die Achse des Eingabearrays, entlang der die Statistik berechnet wird. Die Statistik jedes Achsen-Slices (z. B. Zeile) der Eingabe erscheint dann in einem entsprechenden Element der Ausgabe. Wenn None, wird die Eingabe vor der Berechnung der Statistik geglättet.

method{‘vasicek’, ‘van es’, ‘ebrahimi’, ‘correa’, ‘auto’}, optional

Die Methode zur Schätzung der differentiellen Entropie aus der Stichprobe. Standard ist 'auto'. Siehe Hinweise für weitere Informationen.

nan_policy{‘propagate’, ‘omit’, ‘raise’}

Definiert, wie Eingabe-NaNs behandelt werden.

• propagate: Wenn ein NaN in der Achsen-Slice (z. B. Zeile) vorhanden ist, entlang der die Statistik berechnet wird, wird der entsprechende Eintrag der Ausgabe NaN sein.

• omit: NaNs werden bei der Berechnung weggelassen. Wenn im Achsen-Slice, entlang dem die Statistik berechnet wird, nicht genügend Daten verbleiben, wird der entsprechende Eintrag der Ausgabe NaN sein.

• raise: Wenn ein NaN vorhanden ist, wird ein ValueError ausgelöst.

keepdimsbool, Standard: False

Wenn dies auf True gesetzt ist, bleiben die reduzierten Achsen im Ergebnis als Dimensionen mit der Größe eins erhalten. Mit dieser Option wird das Ergebnis korrekt gegen das Eingabearray gestreut (broadcasted).

Rückgabe:

entropyfloat

Die berechnete differentielle Entropie.

Hinweise

Diese Funktion konvergiert zur wahren differentiellen Entropie im Grenzwert

\[n \to \infty, \quad m \to \infty, \quad \frac{m}{n} \to 0\]

Die optimale Wahl von window_length für eine gegebene Stichprobengröße hängt von der (unbekannten) Verteilung ab. Typischerweise gilt: je glatter die Dichte der Verteilung, desto größer ist der optimale Wert von window_length [1].

Die folgenden Optionen sind für den Parameter method verfügbar.

• 'vasicek' verwendet den in [1] vorgestellten Schätzer. Dies ist einer der ersten und einflussreichsten Schätzer für differentielle Entropie.

• 'van es' verwendet den bias-korrigierten Schätzer, der in [3] vorgestellt wird. Dieser ist nicht nur konsistent, sondern unter bestimmten Bedingungen auch asymptotisch normal.

• 'ebrahimi' verwendet einen in [4] vorgestellten Schätzer, der in Simulationen einen geringeren Bias und mittleren quadratischen Fehler als der Vasicek-Schätzer aufwies.

• 'correa' verwendet den in [5] vorgestellten Schätzer, der auf lokaler linearer Regression basiert. In einer Simulationsstudie zeigte er konsistent einen geringeren mittleren quadratischen Fehler als der Vasicek-Schätzer, ist jedoch teurer in der Berechnung.

• 'auto' wählt die Methode automatisch aus (Standard). Derzeit wählt dies 'van es' für sehr kleine Stichproben (<10), 'ebrahimi' für moderate Stichprobengrößen (11-1000) und 'vasicek' für größere Stichproben. Dieses Verhalten kann sich jedoch in zukünftigen Versionen ändern.

Alle Schätzer sind wie in [6] beschrieben implementiert.

Seit SciPy 1.9 werden np.matrix-Eingaben (für neuen Code nicht empfohlen) vor der Berechnung in np.ndarray konvertiert. In diesem Fall ist die Ausgabe eine Skalar- oder np.ndarray mit geeigneter Form anstelle eines 2D-np.matrix. Ebenso werden, während maskierte Elemente von Masked Arrays ignoriert werden, die Ausgabe eine Skalar- oder np.ndarray anstelle eines Masked Arrays mit mask=False sein.

Referenzen

[1] (1,2)

Vasicek, O. (1976). A test for normality based on sample entropy. Journal of the Royal Statistical Society: Series B (Methodological), 38(1), 54-59.

[2]

Crzcgorzewski, P., & Wirczorkowski, R. (1999). Entropy-based goodness-of-fit test for exponentiality. Communications in Statistics-Theory and Methods, 28(5), 1183-1202.

[3]

Van Es, B. (1992). Estimating functionals related to a density by a class of statistics based on spacings. Scandinavian Journal of Statistics, 61-72.

[4]

Ebrahimi, N., Pflughoeft, K., & Soofi, E. S. (1994). Two measures of sample entropy. Statistics & Probability Letters, 20(3), 225-234.

[5]

Correa, J. C. (1995). A new estimator of entropy. Communications in Statistics-Theory and Methods, 24(10), 2439-2449.

[6]

Noughabi, H. A. (2015). Entropy Estimation Using Numerical Methods. Annals of Data Science, 2(2), 231-241. https://link.springer.com/article/10.1007/s40745-015-0045-9

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> from scipy.stats import differential_entropy, norm

Entropie einer Standardnormalverteilung

>>> rng = np.random.default_rng()
>>> values = rng.standard_normal(100)
>>> differential_entropy(values)
1.3407817436640392

Vergleich mit der wahren Entropie

>>> float(norm.entropy())
1.4189385332046727

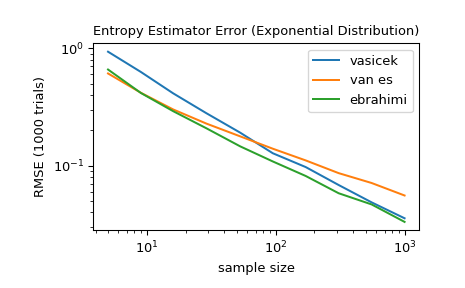
Vergleichen Sie für verschiedene Stichprobengrößen zwischen 5 und 1000 die Genauigkeit der Methoden 'vasicek', 'van es' und 'ebrahimi'. Vergleichen Sie insbesondere den mittleren quadratischen Fehler (über 1000 Durchläufe) zwischen der Schätzung und der wahren differentiellen Entropie der Verteilung.

>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>>
>>>
>>> def rmse(res, expected):
...     '''Root mean squared error'''
...     return np.sqrt(np.mean((res - expected)**2))
>>>
>>>
>>> a, b = np.log10(5), np.log10(1000)
>>> ns = np.round(np.logspace(a, b, 10)).astype(int)
>>> reps = 1000  # number of repetitions for each sample size
>>> expected = stats.expon.entropy()
>>>
>>> method_errors = {'vasicek': [], 'van es': [], 'ebrahimi': []}
>>> for method in method_errors:
...     for n in ns:
...        rvs = stats.expon.rvs(size=(reps, n), random_state=rng)
...        res = stats.differential_entropy(rvs, method=method, axis=-1)
...        error = rmse(res, expected)
...        method_errors[method].append(error)
>>>
>>> for method, errors in method_errors.items():
...     plt.loglog(ns, errors, label=method)
>>>
>>> plt.legend()
>>> plt.xlabel('sample size')
>>> plt.ylabel('RMSE (1000 trials)')
>>> plt.title('Entropy Estimator Error (Exponential Distribution)')

ZurückIn Tab öffnen