gaussian_kde#
- class scipy.stats.gaussian_kde(dataset, bw_method=None, weights=None)[Quelle]#
Repräsentation einer Kernel-Dichteschätzung mit Gaußschen Kernels.
Kernel-Dichteschätzung (Kernel Density Estimation, KDE) ist eine Methode zur nicht-parametrischen Schätzung der Wahrscheinlichkeitsdichtefunktion (PDF) einer Zufallsvariable.
gaussian_kdefunktioniert sowohl für univariate als auch für multivariate Daten. Sie beinhaltet die automatische Bestimmung der Bandbreite. Die Schätzung funktioniert am besten für eine unimodale Verteilung; bimodale oder multimodale Verteilungen neigen dazu, geglättet zu werden.- Parameter:
- datasetarray_like
Datenpunkte zur Schätzung. Im Falle von univariaten Daten ist dies ein 1D-Array, andernfalls ein 2D-Array mit der Form (# Dimensionen, # Datenpunkte).
- bw_methodstr, skalar oder aufrufbar, optional
Die Methode zur Berechnung des Bandbreitenfaktors. Dies kann 'scott', 'silverman', eine skalare Konstante oder eine aufrufbare Funktion sein. Wenn es sich um einen Skalar handelt, wird dieser direkt als factor verwendet. Wenn es sich um eine aufrufbare Funktion handelt, sollte diese eine
gaussian_kde-Instanz als einziges Argument nehmen und einen Skalar zurückgeben. Wenn None (Standard), wird 'scott' verwendet. Siehe Hinweise für weitere Details.- weightsarray_like, optional
Gewichte der Datenpunkte. Dies muss die gleiche Form wie `dataset` haben. Wenn None (Standard), werden die Stichproben als gleich gewichtet angenommen.
- Attribute:
- datasetndarray
Der Datensatz, mit dem
gaussian_kdeinitialisiert wurde.- dint
Anzahl der Dimensionen.
- nint
Anzahl der Datenpunkte.
- neffint
Effektive Anzahl von Datenpunkten.
Hinzugefügt in Version 1.2.0.
- factorfloat
Der Bandbreitenfaktor, der von
covariance_factorerhalten wurde.- covariancendarray
Die Kovarianzmatrix des Kernels; dies ist die Daten-Kovarianzmatrix multipliziert mit dem Quadrat des Bandbreitenfaktors, z. B.
np.cov(dataset) * factor**2.- inv_covndarray
Die Inverse von covariance.
Methoden
evaluate(points)Die geschätzte PDF an einer Reihe von Punkten auswerten.
__call__(points)Die geschätzte PDF an einer Reihe von Punkten auswerten.
integrate_gaussian(mean, cov)Multipliziert die geschätzte Dichte mit einer multivariaten Gaußschen Verteilung und integriert über den gesamten Raum.
integrate_box_1d(low, high)Berechnet das Integral einer 1D-PDF zwischen zwei Grenzen.
integrate_box(low_bounds, high_bounds[, ...])Berechnet das Integral einer PDF über ein rechteckiges Intervall.
integrate_kde(other)Berechnet das Integral des Produkts dieser Kernel-Dichteschätzung mit einer anderen.
pdf(x)Evaluieren Sie die geschätzte PDF an einem bereitgestellten Satz von Punkten.
logpdf(x)Evaluieren Sie den Logarithmus der geschätzten PDF an einem bereitgestellten Satz von Punkten.
resample([size, seed])Zufälliges Ziehen eines Datensatzes aus der geschätzten PDF.
set_bandwidth([bw_method])Berechnen Sie den Bandbreitenfaktor mit der angegebenen Methode.
Berechnet den Bandbreitenfaktor factor.
Hinweise
Die Wahl der Bandbreite hat starken Einfluss auf die von der KDE erhaltene Schätzung (viel stärker als die tatsächliche Form des Kernels). Die Wahl der Bandbreite kann durch eine "Faustregel", durch Kreuzvalidierung, durch "Plug-in-Methoden" oder auf andere Weise erfolgen; siehe [3], [4] für Übersichten.
gaussian_kdeverwendet eine Faustregel, die Standardeinstellung ist Scotts Regel.Scotts Regel [1], implementiert als
scotts_factor, istn**(-1./(d+4)),
mit
nder Anzahl der Datenpunkte unddder Anzahl der Dimensionen. Im Falle von ungleich gewichteten Punkten wirdscotts_factorzuneff**(-1./(d+4)),
mit
neffder effektiven Anzahl von Datenpunkten. Silvermans Vorschlag für *multivariate* Daten [2], implementiert alssilverman_factor, ist(n * (d + 2) / 4.)**(-1. / (d + 4)).
oder im Falle von ungleich gewichteten Punkten
(neff * (d + 2) / 4.)**(-1. / (d + 4)).
Beachten Sie, dass dies nicht dasselbe ist wie "Silvermans Faustregel" [6], welche im univariaten Fall robuster sein kann; siehe Dokumentation der Methode
set_bandwidthfür die Implementierung einer benutzerdefinierten Bandbreitenregel.Gute allgemeine Beschreibungen der Kernel-Dichteschätzung finden Sie in [1] und [2], die Mathematik für diese mehrdimensionale Implementierung finden Sie in [1].
Mit einem Satz gewichteter Stichproben wird die effektive Anzahl von Datenpunkten
neffdefiniert durchneff = sum(weights)^2 / sum(weights^2)
wie in [5] detailliert.
gaussian_kdeunterstützt derzeit keine Daten, die in einem Unterraum geringerer Dimension des Raumes liegen, in dem sie ausgedrückt werden. Für solche Daten sollten Sie eine Hauptkomponentenanalyse / Dimensionsreduktion durchführen undgaussian_kdemit den transformierten Daten verwenden.Referenzen
[1] (1,2,3)D.W. Scott, „Multivariate Density Estimation: Theory, Practice, and Visualization“, John Wiley & Sons, New York, Chicester, 1992.
[2] (1,2)B.W. Silverman, „Density Estimation for Statistics and Data Analysis“, Vol. 26, Monographs on Statistics and Applied Probability, Chapman and Hall, London, 1986.
[3]B.A. Turlach, „Bandwidth Selection in Kernel Density Estimation: A Review“, CORE and Institut de Statistique, Vol. 19, pp. 1-33, 1993.
[4]D.M. Bashtannyk und R.J. Hyndman, „Bandwidth selection for kernel conditional density estimation“, Computational Statistics & Data Analysis, Vol. 36, pp. 279-298, 2001.
[5]Gray P. G., 1969, Journal of the Royal Statistical Society. Series A (General), 132, 272
[6]Kernel-Dichteschätzung. *Wikipedia*. https://en.wikipedia.org/wiki/Kernel_density_estimation
Beispiele
Generieren Sie einige zufällige zweidimensionale Daten
>>> import numpy as np >>> from scipy import stats >>> def measure(n): ... "Measurement model, return two coupled measurements." ... m1 = np.random.normal(size=n) ... m2 = np.random.normal(scale=0.5, size=n) ... return m1+m2, m1-m2
>>> m1, m2 = measure(2000) >>> xmin = m1.min() >>> xmax = m1.max() >>> ymin = m2.min() >>> ymax = m2.max()
Führen Sie eine Kernel-Dichteschätzung für die Daten durch
>>> X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j] >>> positions = np.vstack([X.ravel(), Y.ravel()]) >>> values = np.vstack([m1, m2]) >>> kernel = stats.gaussian_kde(values) >>> Z = np.reshape(kernel(positions).T, X.shape)
Stellen Sie die Ergebnisse grafisch dar
>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> ax.imshow(np.rot90(Z), cmap=plt.cm.gist_earth_r, ... extent=[xmin, xmax, ymin, ymax]) >>> ax.plot(m1, m2, 'k.', markersize=2) >>> ax.set_xlim([xmin, xmax]) >>> ax.set_ylim([ymin, ymax]) >>> plt.show()
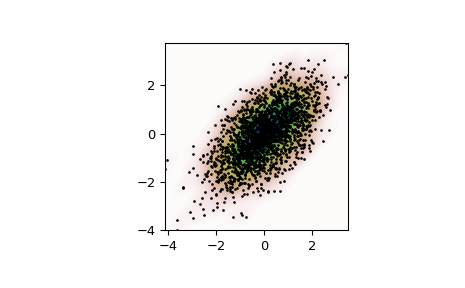
Vergleich mit manueller KDE an einem Punkt
>>> point = [1, 2] >>> mean = values.T >>> cov = kernel.factor**2 * np.cov(values) >>> X = stats.multivariate_normal(cov=cov) >>> res = kernel.pdf(point) >>> ref = X.pdf(point - mean).sum() / len(mean) >>> np.allclose(res, ref) True