scipy.stats.levy_stable

scipy.stats.levy_stable = <scipy.stats._levy_stable.levy_stable_gen object>

Eine Levy-stabile kontinuierliche Zufallsvariable.

Als Instanz der Klasse rv_continuous erbt das Objekt levy_stable von ihr eine Sammlung von generischen Methoden (siehe unten für die vollständige Liste) und vervollständigt sie mit Details, die für diese spezielle Verteilung spezifisch sind.

Methoden

rvs(alpha, beta, loc=0, scale=1, size=1, random_state=None)	Zufallsvariaten.
pdf(x, alpha, beta, loc=0, scale=1)	Wahrscheinlichkeitsdichtefunktion.
logpdf(x, alpha, beta, loc=0, scale=1)	Logarithmus der Wahrscheinlichkeitsdichtefunktion.
cdf(x, alpha, beta, loc=0, scale=1)	Kumulative Verteilungsfunktion.
logcdf(x, alpha, beta, loc=0, scale=1)	Logarithmus der kumulativen Verteilungsfunktion.
sf(x, alpha, beta, loc=0, scale=1)	Überlebensfunktion (auch definiert als 1 - cdf, aber sf ist manchmal genauer).
logsf(x, alpha, beta, loc=0, scale=1)	Logarithmus der Überlebensfunktion.
ppf(q, alpha, beta, loc=0, scale=1)	Perzentilpunktfunktion (Umkehrung von cdf — Perzentile).
isf(q, alpha, beta, loc=0, scale=1)	Umgekehrte Überlebensfunktion (Umkehrung von sf).
moment(order, alpha, beta, loc=0, scale=1)	Nichtzentrales Moment der angegebenen Ordnung.
stats(alpha, beta, loc=0, scale=1, moments=’mv’)	Mittelwert(‚m‘), Varianz(‚v‘), Schiefe(‚s‘) und/oder Kurtosis(‚k‘).
entropy(alpha, beta, loc=0, scale=1)	(Differential-)Entropie der RV.
fit(data)	Parameterschätzungen für generische Daten. Siehe scipy.stats.rv_continuous.fit für eine detaillierte Dokumentation der Schlüsselwortargumente.
expect(func, args=(alpha, beta), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)	Erwartungswert einer Funktion (einer Variablen) bezüglich der Verteilung.
median(alpha, beta, loc=0, scale=1)	Median der Verteilung.
mean(alpha, beta, loc=0, scale=1)	Mittelwert der Verteilung.
var(alpha, beta, loc=0, scale=1)	Varianz der Verteilung.
std(alpha, beta, loc=0, scale=1)	Standardabweichung der Verteilung.
interval(confidence, alpha, beta, loc=0, scale=1)	Konfidenzintervall mit gleichen Flächen um den Median.

Siehe auch

levy, levy_l, cauchy, norm

Hinweise

Die Verteilung für levy_stable hat die charakteristische Funktion

\[\varphi(t, \alpha, \beta, c, \mu) = e^{it\mu -|ct|^{\alpha}(1-i\beta\operatorname{sign}(t)\Phi(\alpha, t))}\]

wobei zwei verschiedene Parametrisierungen unterstützt werden. Die erste \(S_1\)

\[\begin{split}\Phi = \begin{cases} \tan \left({\frac {\pi \alpha }{2}}\right)&\alpha \neq 1\\ -{\frac {2}{\pi }}\log |t|&\alpha =1 \end{cases}\end{split}\]

Die zweite \(S_0\)

\[\begin{split}\Phi = \begin{cases} -\tan \left({\frac {\pi \alpha }{2}}\right)(|ct|^{1-\alpha}-1) &\alpha \neq 1\\ -{\frac {2}{\pi }}\log |ct|&\alpha =1 \end{cases}\end{split}\]

Die Wahrscheinlichkeitsdichtefunktion für levy_stable ist

\[f(x) = \frac{1}{2\pi}\int_{-\infty}^\infty \varphi(t)e^{-ixt}\,dt\]

wobei \(-\infty < t < \infty\). Dieses Integral hat keine bekannte geschlossene Form.

levy_stable verallgemeinert mehrere Verteilungen. Wo möglich, sollten diese stattdessen verwendet werden. Insbesondere, wenn die Formparameter die Werte in der folgenden Tabelle annehmen, sollte die entsprechende äquivalente Verteilung verwendet werden.

alpha	beta	Äquivalent
1/2	-1	levy_l
1/2	1	levy
1	0	cauchy
2	beliebig	norm (mit scale=sqrt(2))

Die Auswertung der Dichte verwendet standardmäßig Nolans stückweise Integrationsmethode mit der Zolotarev \(M\)-Parametrisierung. Es gibt auch die Option, durch direkte numerische Integration der Standardparametrisierung der charakteristischen Funktion zu werten oder durch die FFT der charakteristischen Funktion zu werten.

Die Standardmethode kann durch Setzen der Klassenvariablen levy_stable.pdf_default_method auf einen der Werte ‘piecewise’ für Nolans Ansatz, ‘dni’ für direkte numerische Integration oder ‘fft-simpson’ für den FFT-basierten Ansatz geändert werden. Aus Gründen der Abwärtskompatibilität sind die Methoden ‘best’ und ‘zolotarev’ äquivalent zu ‘piecewise’ und die Methode ‘quadrature’ ist äquivalent zu ‘dni’.

Die Parametrisierung kann durch Setzen der Klassenvariablen levy_stable.parameterization auf ‘S0’ oder ‘S1’ geändert werden. Der Standard ist ‘S1’.

Um die Leistung der stückweisen und direkten numerischen Integration zu verbessern, können Sie levy_stable.quad_eps (Standardwert 1.2e-14) angeben. Dies wird sowohl als absolute als auch als relative Quadraturtoleranz für die direkte numerische Integration und als relative Quadraturtoleranz für die stückweise Methode verwendet. Sie können auch levy_stable.piecewise_x_tol_near_zeta (Standardwert 0.005) angeben, wie nah x an zeta sein muss, bevor es als gleich x betrachtet wird [NO]. Die genaue Prüfung ist abs(x0 - zeta) < piecewise_x_tol_near_zeta*alpha**(1/alpha). Sie können auch levy_stable.piecewise_alpha_tol_near_one (Standardwert 0.005) angeben, wie nah alpha an 1 sein muss, bevor es als gleich 1 betrachtet wird.

Um die Genauigkeit der FFT-Berechnung zu erhöhen, können Sie levy_stable.pdf_fft_grid_spacing (Standardwert 0.001) und pdf_fft_n_points_two_power (Standardwert None, was bedeutet, dass ein Wert berechnet wird, der den Eingabebereich ausreichend abdeckt) angeben.

Weitere Kontrolle über die FFT-Berechnung ist verfügbar, indem Sie pdf_fft_interpolation_degree (Standardwert 3) für die Spline-Ordnung und pdf_fft_interpolation_level für die Bestimmung der Anzahl der Punkte in der Newton-Cotes-Formel bei der Approximation der charakteristischen Funktion (als experimentell betrachtet) festlegen.

Die Auswertung der CDF verwendet standardmäßig Nolans stückweise Integrationsmethode mit der Zolotarev \(S_0\)-Parametrisierung. Es gibt auch die Option, durch Integration eines interpolierten Splines der PDF, der mittels der FFT-Methode berechnet wurde, zu werten. Die Einstellungen, die die FFT-Berechnung beeinflussen, sind die gleichen wie für die PDF-Berechnung. Die Standard-CDF-Methode kann durch Setzen von levy_stable.cdf_default_method auf entweder ‘piecewise’ oder ‘fft-simpson’ geändert werden. Für CDF-Berechnungen ist die Zolotarev-Methode in Bezug auf die Genauigkeit überlegen, daher ist FFT standardmäßig deaktiviert.

Die Schätzung für die Anpassung verwendet die Quantilschätzmethode in [MC]. Die MLE-Schätzung von Parametern in der Fit-Methode verwendet zunächst diese Quantilschätzung. Beachten Sie, dass MLE nicht immer konvergiert, wenn für die PDF-Berechnungen FFT verwendet wird; dies ist der Fall, wenn alpha <= 1 ist, wo der FFT-Ansatz keine guten Näherungen liefert.

Jeder nicht-fehlende Wert für das Attribut levy_stable.pdf_fft_min_points_threshold setzt levy_stable.pdf_default_method auf ‘fft-simpson’, wenn keine gültige Standardmethode anderweitig gesetzt ist.

Warnung

Für PDF-Berechnungen wird die FFT-Berechnung als experimentell betrachtet.

Für CDF-Berechnungen wird die FFT-Berechnung als experimentell betrachtet. Verwenden Sie stattdessen Zolotarevs Methode (Standard).

Die oben genannte Wahrscheinlichkeitsdichte ist in der „standardisierten“ Form definiert. Um die Verteilung zu verschieben und/oder zu skalieren, verwenden Sie die Parameter loc und scale. Im Allgemeinen ist levy_stable.pdf(x, alpha, beta, loc, scale) identisch äquivalent zu levy_stable.pdf(y, alpha, beta) / scale mit y = (x - loc) / scale, außer in der \(S_1\)-Parametrisierung, wenn alpha == 1. In diesem Fall ist levy_stable.pdf(x, alpha, beta, loc, scale) identisch äquivalent zu levy_stable.pdf(y, alpha, beta) / scale mit y = (x - loc - 2 * beta * scale * np.log(scale) / np.pi) / scale. Siehe [NO2] Definition 1.8 für weitere Informationen. Beachten Sie, dass das Verschieben des Ortes einer Verteilung sie nicht zu einer „nichtzentralen“ Verteilung macht.

Referenzen

[MC]

McCulloch, J., 1986. Simple consistent estimators of stable distribution parameters. Communications in Statistics - Simulation and Computation 15, 11091136.

[WZ]

Wang, Li und Zhang, Ji-Hong, 2008. Simpson’s rule based FFT method to compute densities of stable distribution.

[NO]

Nolan, J., 1997. Numerical Calculation of Stable Densities and distributions Functions.

[NO2]

Nolan, J., 2018. Stable Distributions: Models for Heavy Tailed Data.

[HO]

Hopcraft, K. I., Jakeman, E., Tanner, R. M. J., 1999. Lévy random walks with fluctuating step number and multiscale behavior.

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> from scipy.stats import levy_stable
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)

Ermitteln Sie den Träger (Support)

>>> alpha, beta = 1.8, -0.5
>>> lb, ub = levy_stable.support(alpha, beta)

Berechnen Sie die ersten vier Momente

>>> mean, var, skew, kurt = levy_stable.stats(alpha, beta, moments='mvsk')

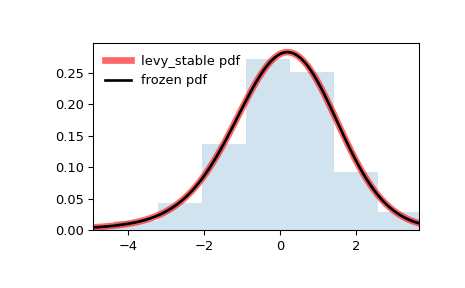
Zeigen Sie die Wahrscheinlichkeitsdichtefunktion (pdf) an

>>> x = np.linspace(levy_stable.ppf(0.01, alpha, beta),
...                 levy_stable.ppf(0.99, alpha, beta), 100)
>>> ax.plot(x, levy_stable.pdf(x, alpha, beta),
...        'r-', lw=5, alpha=0.6, label='levy_stable pdf')

Alternativ kann das Verteilungsobjekt (als Funktion) aufgerufen werden, um die Form-, Orts- und Skalierungsparameter festzulegen. Dies gibt ein „eingefrorenes“ RV-Objekt zurück, das die angegebenen Parameter beibehält.

Frieren Sie die Verteilung ein und zeigen Sie die eingefrorene pdf an

>>> rv = levy_stable(alpha, beta)
>>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')

Überprüfen Sie die Genauigkeit von cdf und ppf

>>> vals = levy_stable.ppf([0.001, 0.5, 0.999], alpha, beta)
>>> np.allclose([0.001, 0.5, 0.999], levy_stable.cdf(vals, alpha, beta))
True

Generieren Sie Zufallszahlen

>>> r = levy_stable.rvs(alpha, beta, size=1000)

Und vergleichen Sie das Histogramm

>>> ax.hist(r, density=True, bins='auto', histtype='stepfilled', alpha=0.2)
>>> ax.set_xlim([x[0], x[-1]])
>>> ax.legend(loc='best', frameon=False)
>>> plt.show()

ZurückIn Tab öffnen