linregress#
- scipy.stats.linregress(x, y, alternative='two-sided', *, axis=0, nan_policy='propagate', keepdims=False)[Quellcode]#
Berechnet eine lineare Regressionsanalyse nach der Methode der kleinsten Quadrate für zwei Messreihen.
- Parameter:
- x, yarray_like
Zwei Messreihen. Beide Arrays sollten die gleiche Länge N haben.
- alternative{‘zweiseitig’, ‘kleiner’, ‘größer’}, optional
Definiert die Alternativhypothese. Standard ist ‘zweiseitig’. Folgende Optionen sind verfügbar
‘two-sided’: die Steigung der Regressionsgerade ist ungleich Null
‘less’: die Steigung der Regressionsgerade ist kleiner als Null
‘greater’: die Steigung der Regressionsgerade ist größer als Null
Hinzugefügt in Version 1.7.0.
- axisint oder None, Standard: 0
Wenn es sich um eine ganze Zahl handelt, ist dies die Achse des Eingabearrays, entlang der die Statistik berechnet wird. Die Statistik jedes Achsen-Slices (z. B. Zeile) der Eingabe erscheint dann in einem entsprechenden Element der Ausgabe. Wenn
None, wird die Eingabe vor der Berechnung der Statistik geglättet.- nan_policy{‘propagate’, ‘omit’, ‘raise’}
Definiert, wie Eingabe-NaNs behandelt werden.
propagate: Wenn ein NaN in der Achsen-Slice (z. B. Zeile) vorhanden ist, entlang der die Statistik berechnet wird, wird der entsprechende Eintrag der Ausgabe NaN sein.omit: NaNs werden bei der Berechnung weggelassen. Wenn im Achsen-Slice, entlang dem die Statistik berechnet wird, nicht genügend Daten verbleiben, wird der entsprechende Eintrag der Ausgabe NaN sein.raise: Wenn ein NaN vorhanden ist, wird einValueErrorausgelöst.
- keepdimsbool, Standard: False
Wenn dies auf True gesetzt ist, bleiben die reduzierten Achsen im Ergebnis als Dimensionen mit der Größe eins erhalten. Mit dieser Option wird das Ergebnis korrekt gegen das Eingabearray gestreut (broadcasted).
- Rückgabe:
- result
LinregressResultInstanz Der Rückgabewert ist ein Objekt mit folgenden Attributen:
- slopefloat
Steigung der Regressionsgerade.
- interceptfloat
Achsenabschnitt der Regressionsgerade.
- rvaluefloat
Der Pearson-Korrelationskoeffizient. Das Quadrat von
rvalueist gleich dem Bestimmtheitsmaß.- pvaluefloat
Der p-Wert für einen Hypothesentest, dessen Nullhypothese lautet, dass die Steigung Null ist, unter Verwendung des Wald-Tests mit t-Verteilung der Teststatistik. Siehe alternative oben für alternative Hypothesen.
- stderrfloat
Standardfehler der geschätzten Steigung (Gradient), unter der Annahme der Normalverteilung der Residuen.
- intercept_stderrfloat
Standardfehler des geschätzten Achsenabschnitts, unter der Annahme der Normalverteilung der Residuen.
- result
Siehe auch
scipy.optimize.curve_fitVerwendet nichtlineare kleinste Quadrate, um eine Funktion an Daten anzupassen.
scipy.optimize.leastsqMinimiert die Summe der Quadrate eines Gleichungssystems.
Hinweise
Aus Kompatibilitätsgründen mit älteren SciPy-Versionen verhält sich der Rückgabewert wie ein
namedtupleder Länge 5 mit den Feldernslope,intercept,rvalue,pvalueundstderr, sodass man weiterhin schreiben kannslope, intercept, r, p, se = linregress(x, y)
Mit diesem Stil ist jedoch der Standardfehler des Achsenabschnitts nicht verfügbar. Um Zugriff auf alle berechneten Werte, einschließlich des Standardfehlers des Achsenabschnitts, zu haben, verwenden Sie den Rückgabewert als Objekt mit Attributen, z. B.
result = linregress(x, y) print(result.intercept, result.intercept_stderr)
Seit SciPy 1.9 werden
np.matrix-Eingaben (für neuen Code nicht empfohlen) vor der Berechnung innp.ndarraykonvertiert. In diesem Fall ist die Ausgabe eine Skalar- odernp.ndarraymit geeigneter Form anstelle eines 2D-np.matrix. Ebenso werden, während maskierte Elemente von Masked Arrays ignoriert werden, die Ausgabe eine Skalar- odernp.ndarrayanstelle eines Masked Arrays mitmask=Falsesein.Beispiele
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy import stats >>> rng = np.random.default_rng()
Generieren Sie einige Daten
>>> x = rng.random(10) >>> y = 1.6*x + rng.random(10)
Führen Sie die lineare Regression durch
>>> res = stats.linregress(x, y)
Bestimmtheitsmaß (R-Quadrat)
>>> print(f"R-squared: {res.rvalue**2:.6f}") R-squared: 0.717533
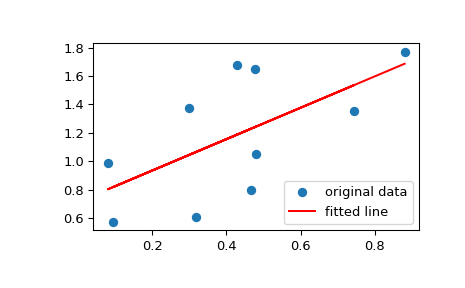
Zeichnen Sie die Daten zusammen mit der angepassten Geraden
>>> plt.plot(x, y, 'o', label='original data') >>> plt.plot(x, res.intercept + res.slope*x, 'r', label='fitted line') >>> plt.legend() >>> plt.show()
Berechnen Sie das 95% Konfidenzintervall für Steigung und Achsenabschnitt
>>> # Two-sided inverse Students t-distribution >>> # p - probability, df - degrees of freedom >>> from scipy.stats import t >>> tinv = lambda p, df: abs(t.ppf(p/2, df))
>>> ts = tinv(0.05, len(x)-2) >>> print(f"slope (95%): {res.slope:.6f} +/- {ts*res.stderr:.6f}") slope (95%): 1.453392 +/- 0.743465 >>> print(f"intercept (95%): {res.intercept:.6f}" ... f" +/- {ts*res.intercept_stderr:.6f}") intercept (95%): 0.616950 +/- 0.544475