logrank#
- scipy.stats.logrank(x, y, alternative='two-sided')[Quelle]#
Vergleichen Sie die Überlebensverteilungen von zwei Stichproben mithilfe des Logrank-Tests.
- Parameter:
- x, yarray_like oder CensoredData
Zu vergleichende Stichproben basierend auf ihren empirischen Überlebensfunktionen.
- alternative{‘zweiseitig’, ‘kleiner’, ‘größer’}, optional
Definiert die alternative Hypothese.
Die Nullhypothese ist, dass die Überlebensverteilungen der beiden Gruppen, sagen wir X und Y, identisch sind.
Die folgenden alternativen Hypothesen [4] sind verfügbar (Standard ist 'two-sided')
'two-sided': die Überlebensverteilungen der beiden Gruppen sind nicht identisch.
'less': Das Überleben der Gruppe X wird bevorzugt: die Ausfallratenfunktion der Gruppe X ist zu bestimmten Zeiten geringer als die der Gruppe Y.
'greater': Das Überleben der Gruppe Y wird bevorzugt: die Ausfallratenfunktion der Gruppe X ist zu bestimmten Zeiten größer als die der Gruppe Y.
- Rückgabe:
- resLogRankResult
Ein Objekt, das Attribute enthält
- statisticfloat ndarray
Die berechnete Statistik (unten definiert). Ihr Betrag ist die Quadratwurzel des Betrags, der von den meisten anderen Logrank-Testimplementierungen zurückgegeben wird.
- pvaluefloat ndarray
Der berechnete p-Wert des Tests.
Siehe auch
Hinweise
Der Logrank-Test [1] vergleicht die beobachtete Anzahl von Ereignissen mit der erwarteten Anzahl von Ereignissen unter der Nullhypothese, dass die beiden Stichproben aus derselben Verteilung gezogen wurden. Die Statistik lautet
\[Z_i = \frac{\sum_{j=1}^J(O_{i,j}-E_{i,j})}{\sqrt{\sum_{j=1}^J V_{i,j}}} \rightarrow \mathcal{N}(0,1)\]wo
\[E_{i,j} = O_j \frac{N_{i,j}}{N_j}, \qquad V_{i,j} = E_{i,j} \left(\frac{N_j-O_j}{N_j}\right) \left(\frac{N_j-N_{i,j}}{N_j-1}\right),\]\(i\) bezeichnet die Gruppe (d.h. sie kann Werte \(x\) oder \(y\) annehmen, oder sie kann weggelassen werden, um sich auf die kombinierte Stichprobe zu beziehen) \(j\) bezeichnet die Zeit (zu der ein Ereignis auftrat), \(N\) ist die Anzahl der zu Beginn eines Ereignisses noch gefährdeten Subjekte und \(O\) ist die beobachtete Anzahl von Ereignissen zu diesem Zeitpunkt.
Die von
logrankzurückgegebenestatistic\(Z_x\) ist die (vorzeichenbehaftete) Quadratwurzel der Statistik, die von vielen anderen Implementierungen zurückgegeben wird. Unter der Nullhypothese ist \(Z_x**2\) asymptotisch nach der Chi-Quadrat-Verteilung mit einem Freiheitsgrad verteilt. Folglich ist \(Z_x\) asymptotisch nach der Standardnormalverteilung verteilt. Der Vorteil der Verwendung von \(Z_x\) ist, dass die Vorzeicheninformation (d.h. ob die beobachtete Anzahl von Ereignissen tendenziell geringer oder größer ist als die unter der Nullhypothese erwartete Anzahl) erhalten bleibt, was esscipy.stats.logrankermöglicht, einseitige alternative Hypothesen anzubieten.Referenzen
[1]Mantel N. „Evaluation of survival data and two new rank order statistics arising in its consideration.“ Cancer Chemotherapy Reports, 50(3):163-170, PMID: 5910392, 1966
[2]Bland, Altman, „The logrank test“, BMJ, 328:1073, DOI:10.1136/bmj.328.7447.1073, 2004
[3]„Logrank test“, Wikipedia, https://en.wikipedia.org/wiki/Logrank_test
[4]Brown, Mark. „On the choice of variance for the log rank test.“ Biometrika 71.1 (1984): 65-74.
[5]Klein, John P., und Melvin L. Moeschberger. Survival analysis: techniques for censored and truncated data. Vol. 1230. New York: Springer, 2003.
Beispiele
Referenz [2] verglich die Überlebenszeiten von Patienten mit zwei verschiedenen Arten von rezidivierenden malignen Gliomen. Die nachfolgenden Stichproben zeichnen die Zeit (Anzahl der Wochen) auf, die jeder Patient an der Studie teilgenommen hat. Die Klasse
scipy.stats.CensoredDatawird verwendet, da die Daten rechtszensiert sind: die unzensierten Beobachtungen entsprechen beobachteten Todesfällen, während die zensierten Beobachtungen dem Grund entsprechen, warum der Patient die Studie aus anderen Gründen verlassen hat.>>> from scipy import stats >>> x = stats.CensoredData( ... uncensored=[6, 13, 21, 30, 37, 38, 49, 50, ... 63, 79, 86, 98, 202, 219], ... right=[31, 47, 80, 82, 82, 149] ... ) >>> y = stats.CensoredData( ... uncensored=[10, 10, 12, 13, 14, 15, 16, 17, 18, 20, 24, 24, ... 25, 28,30, 33, 35, 37, 40, 40, 46, 48, 76, 81, ... 82, 91, 112, 181], ... right=[34, 40, 70] ... )
Wir können die empirischen Überlebensfunktionen beider Gruppen wie folgt berechnen und visualisieren.
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> ax = plt.subplot() >>> ecdf_x = stats.ecdf(x) >>> ecdf_x.sf.plot(ax, label='Astrocytoma') >>> ecdf_y = stats.ecdf(y) >>> ecdf_y.sf.plot(ax, label='Glioblastoma') >>> ax.set_xlabel('Time to death (weeks)') >>> ax.set_ylabel('Empirical SF') >>> plt.legend() >>> plt.show()
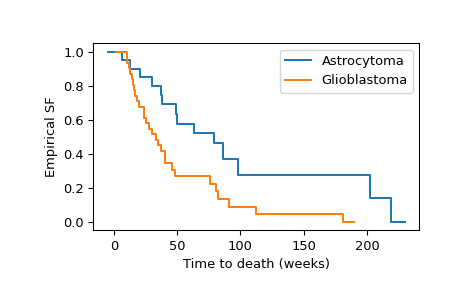
Die visuelle Inspektion der empirischen Überlebensfunktionen legt nahe, dass die Überlebenszeiten zwischen den beiden Gruppen tendenziell unterschiedlich sind. Um formal zu prüfen, ob der Unterschied auf dem 1%-Niveau signifikant ist, verwenden wir den Logrank-Test.
>>> res = stats.logrank(x=x, y=y) >>> res.statistic -2.73799 >>> res.pvalue 0.00618
Der p-Wert ist kleiner als 1%, daher können wir die Daten als Beweis gegen die Nullhypothese werten, zugunsten der Alternative, dass es einen Unterschied zwischen den beiden Überlebensfunktionen gibt.