scipy.stats.mstats.

linregress

scipy.stats.mstats.linregress(x, y=None)

Berechnet eine lineare Regressionsanalyse nach der Methode der kleinsten Quadrate für zwei Messreihen.

Parameter:

x, yarray_like

Zwei Messreihen. Beide Arrays sollten die gleiche Länge N haben. Wenn nur x gegeben ist (und y=None), dann muss es ein zweidimensionales Array sein, bei dem eine Dimension die Länge 2 hat. Die beiden Messreihen werden dann durch Aufteilen des Arrays entlang der Länge-2-Dimension ermittelt. In dem Fall, dass y=None und x ein 2xN-Array ist, ist linregress(x) äquivalent zu linregress(x[0], x[1]).

Rückgabe:

ErgebnisLinregressResult Instanz

Der Rückgabewert ist ein Objekt mit folgenden Attributen:

slopefloat

Steigung der Regressionsgeraden.

interceptfloat

Achsenabschnitt der Regressionsgeraden.

rvaluefloat

Der Pearson-Korrelationskoeffizient. Das Quadrat von rvalue ist gleich dem Bestimmtheitsmaß.

pvaluefloat

Der p-Wert für einen Hypothesentest, dessen Nullhypothese besagt, dass die Steigung Null ist, unter Verwendung des Wald-Tests mit t-Verteilung der Teststatistik. Siehe alternative oben für alternative Hypothesen.

stderrfloat

Standardfehler der geschätzten Steigung (Gradient), unter der Annahme von Residuen-Normalität.

intercept_stderrfloat

Standardfehler des geschätzten Achsenabschnitts, unter der Annahme von Residuen-Normalität.

Siehe auch

scipy.optimize.curve_fit

Verwendet nichtlineare Kleinste-Quadrate-Anpassung einer Funktion an Daten.

scipy.optimize.leastsq

Minimiert die Summe der Quadrate eines Gleichungssystems.

Hinweise

Fehlende Werte werden paarweise betrachtet: Wenn ein Wert in x fehlt, wird der entsprechende Wert in y maskiert.

Zur Kompatibilität mit älteren Versionen von SciPy verhält sich der Rückgabewert wie ein namedtuple der Länge 5 mit den Feldern slope, intercept, rvalue, pvalue und stderr, sodass man weiterhin schreiben kann

slope, intercept, r, p, se = linregress(x, y)

Mit diesem Stil ist jedoch der Standardfehler des Achsenabschnitts nicht verfügbar. Um Zugriff auf alle berechneten Werte zu haben, einschließlich des Standardfehlers des Achsenabschnitts, verwenden Sie den Rückgabewert als Objekt mit Attributen, z. B.

result = linregress(x, y)
print(result.intercept, result.intercept_stderr)

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> rng = np.random.default_rng()

Erzeuge einige Daten

>>> x = rng.random(10)
>>> y = 1.6*x + rng.random(10)

Führe die lineare Regression durch

>>> res = stats.mstats.linregress(x, y)

Bestimmtheitsmaß (R-Quadrat)

>>> print(f"R-squared: {res.rvalue**2:.6f}")
R-squared: 0.717533

Zeichne die Daten zusammen mit der angepassten Linie

>>> plt.plot(x, y, 'o', label='original data')
>>> plt.plot(x, res.intercept + res.slope*x, 'r', label='fitted line')
>>> plt.legend()
>>> plt.show()

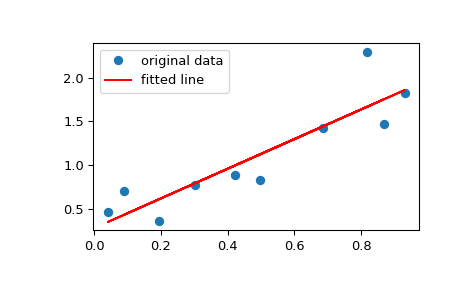
Berechne das 95%-Konfidenzintervall für Steigung und Achsenabschnitt

>>> # Two-sided inverse Students t-distribution
>>> # p - probability, df - degrees of freedom
>>> from scipy.stats import t
>>> tinv = lambda p, df: abs(t.ppf(p/2, df))

>>> ts = tinv(0.05, len(x)-2)
>>> print(f"slope (95%): {res.slope:.6f} +/- {ts*res.stderr:.6f}")
slope (95%): 1.453392 +/- 0.743465
>>> print(f"intercept (95%): {res.intercept:.6f}"
...       f" +/- {ts*res.intercept_stderr:.6f}")
intercept (95%): 0.616950 +/- 0.544475

ZurückIn Tab öffnen