scipy.stats.multivariate_normal

scipy.stats.multivariate_normal = <scipy.stats._multivariate.multivariate_normal_gen object>

Eine multivariate Normalverteilung-Zufallsvariable.

Das Schlüsselwort mean spezifiziert den Mittelwert. Das Schlüsselwort cov spezifiziert die Kovarianzmatrix.

Parameter:

meanarray_like, Standard: [0]

Mittelwert der Verteilung.

covarray_like oder Covariance, Standard: [1]

Symmetrische positiv (semi-)definite Kovarianzmatrix der Verteilung.

allow_singularbool, Standard: False

Ob eine singuläre Kovarianzmatrix erlaubt werden soll. Dies wird ignoriert, wenn cov ein Covariance-Objekt ist.

seed{None, int, np.random.RandomState, np.random.Generator}, optional

Wird zum Ziehen von Zufallsvarianten verwendet. Wenn seed None ist, wird die RandomState Singleton verwendet. Wenn seed eine Ganzzahl ist, wird eine neue RandomState-Instanz verwendet, die mit seed initialisiert wird. Wenn seed bereits eine RandomState- oder Generator-Instanz ist, wird dieses Objekt verwendet. Standard ist None.

Methoden

pdf(x, mean=None, cov=1, allow_singular=False)	Wahrscheinlichkeitsdichtefunktion.
logpdf(x, mean=None, cov=1, allow_singular=False)	Logarithmus der Wahrscheinlichkeitsdichtefunktion.
cdf(x, mean=None, cov=1, allow_singular=False, maxpts=1000000*dim, abseps=1e-5, releps=1e-5, lower_limit=None)	Kumulative Verteilungsfunktion.
logcdf(x, mean=None, cov=1, allow_singular=False, maxpts=1000000*dim, abseps=1e-5, releps=1e-5)	Logarithmus der kumulativen Verteilungsfunktion.
rvs(mean=None, cov=1, size=1, random_state=None)	Zufällige Stichproben aus einer multivariaten Normalverteilung ziehen.
entropy(mean=None, cov=1)	Berechnet die differentielle Entropie der multivariaten Normalverteilung.
fit(x, fix_mean=None, fix_cov=None)	Passt eine multivariate Normalverteilung an Daten an.

Hinweise

Das Setzen des Parameters mean auf None entspricht einem Nullvektor für mean. Der Parameter cov kann ein Skalar sein, in diesem Fall ist die Kovarianzmatrix die Identität multipliziert mit diesem Wert, ein Vektor von Diagonaleinträgen für die Kovarianzmatrix, eine zweidimensionale array_like oder ein Covariance-Objekt.

Die Kovarianzmatrix cov kann eine Instanz einer Unterklasse von Covariance sein, z.B. scipy.stats.CovViaPrecision. In diesem Fall wird allow_singular ignoriert.

Andernfalls muss cov eine symmetrische positiv semidefinite Matrix sein, wenn allow_singular True ist; sie muss (strikt) positiv definit sein, wenn allow_singular False ist. Symmetrie wird nicht überprüft; nur der untere dreieckige Teil wird verwendet. Die Determinante und Inverse von cov werden als Pseudo-Determinante bzw. Pseudo-Inverse berechnet, sodass cov keinen vollen Rang haben muss.

Die Wahrscheinlichkeitsdichtefunktion für multivariate_normal lautet

\[f(x) = \frac{1}{\sqrt{(2 \pi)^k \det \Sigma}} \exp\left( -\frac{1}{2} (x - \mu)^T \Sigma^{-1} (x - \mu) \right),\]

wobei \(\mu\) der Mittelwert, \(\Sigma\) die Kovarianzmatrix und \(k\) der Rang von \(\Sigma\) ist. Im Falle eines singulären \(\Sigma\) erweitert SciPy diese Definition gemäß [1].

Hinzugefügt in Version 0.14.0.

Referenzen

[1]

Multivariate Normalverteilung - Degenerierter Fall, Wikipedia, https://en.wikipedia.org/wiki/Multivariate_normal_distribution#Degenerate_case

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import multivariate_normal

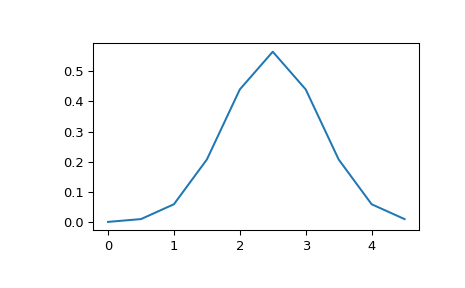
>>> x = np.linspace(0, 5, 10, endpoint=False)
>>> y = multivariate_normal.pdf(x, mean=2.5, cov=0.5); y
array([ 0.00108914,  0.01033349,  0.05946514,  0.20755375,  0.43939129,
        0.56418958,  0.43939129,  0.20755375,  0.05946514,  0.01033349])
>>> fig1 = plt.figure()
>>> ax = fig1.add_subplot(111)
>>> ax.plot(x, y)
>>> plt.show()

Alternativ kann das Objekt (als Funktion) aufgerufen werden, um die Parameter für Mittelwert und Kovarianz festzulegen, wodurch eine "eingefrorene" multivariate Normalverteilung-Zufallsvariable zurückgegeben wird.

>>> rv = multivariate_normal(mean=None, cov=1, allow_singular=False)
>>> # Frozen object with the same methods but holding the given
>>> # mean and covariance fixed.

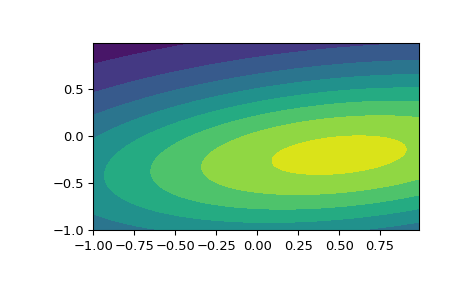
Die Eingangsquantile können jede beliebige Array-Form haben, solange die letzte Achse die Komponenten beschreibt. Dies ermöglicht uns beispielsweise, die eingefrorene pdf für eine nicht-isotrope Zufallsvariable in 2D wie folgt anzuzeigen:

>>> x, y = np.mgrid[-1:1:.01, -1:1:.01]
>>> pos = np.dstack((x, y))
>>> rv = multivariate_normal([0.5, -0.2], [[2.0, 0.3], [0.3, 0.5]])
>>> fig2 = plt.figure()
>>> ax2 = fig2.add_subplot(111)
>>> ax2.contourf(x, y, rv.pdf(pos))

ZurückIn Tab öffnen