scipy.stats.normal_inverse_gamma#
- scipy.stats.normal_inverse_gamma = <scipy.stats._multivariate.normal_inverse_gamma_gen object>[Quelle]#
Normal-Invers-Gamma-Verteilung.
Die Normal-Invers-Gamma-Verteilung ist die konjugierte Prior-Verteilung für eine Normalverteilung mit unbekanntem Mittelwert und unbekannter Varianz.
- Parameter:
- mu, lmbda, a, barray_like
Formparameter der Verteilung. Siehe Anmerkungen.
- seed{None, int, np.random.RandomState, np.random.Generator}, optional
Wird zum Ziehen von Zufallsvarianten verwendet. Wenn seed None ist, wird die RandomState Singleton verwendet. Wenn seed eine Ganzzahl ist, wird eine neue
RandomState-Instanz verwendet, die mit seed initialisiert wird. Wenn seed bereits eineRandomState- oderGenerator-Instanz ist, wird dieses Objekt verwendet. Standard ist None.
Methoden
pdf(x, s2, mu=0, lmbda=1, a=1, b=1)
Wahrscheinlichkeitsdichtefunktion.
logpdf(x, s2, mu=0, lmbda=1, a=1, b=1)
Logarithmus der Wahrscheinlichkeitsdichtefunktion.
mean(mu=0, lmbda=1, a=1, b=1)
Mittelwert der Verteilung.
var(mu=0, lmbda=1, a=1, b=1)
Varianz der Verteilung.
rvs(mu=0, lmbda=1, a=1, b=1, size=None, random_state=None)
Zufällige Stichproben ziehen.
Hinweise
Die Wahrscheinlichkeitsdichtefunktion von
normal_inverse_gammaist\[f(x, \sigma^2; \mu, \lambda, \alpha, \beta) = \frac{\sqrt{\lambda}}{\sqrt{2 \pi \sigma^2}} \frac{\beta^\alpha}{\Gamma(\alpha)} \left( \frac{1}{\sigma^2} \right)^{\alpha + 1} \exp \left(- \frac{2 \beta + \lambda (x - \mu)^2} {2 \sigma^2} \right)\]wobei alle Parameter reell und endlich sind und \(\sigma^2 > 0\), \(\lambda > 0\), \(\alpha > 0\) und \(\beta > 0\).
Die Methoden
normal_inverse_gamma.pdfundnormal_inverse_gamma.logpdfakzeptieren x und s2 für die Argumente \(x\) und \(\sigma^2\). Alle Methoden akzeptieren mu, lmbda, a und b für die Formparameter \(\mu\), \(\lambda\), \(\alpha\) und \(\beta\).Hinzugefügt in Version 1.15.
Referenzen
[1]Normal-Invers-Gamma-Verteilung, Wikipedia, https://en.wikipedia.org/wiki/Normal-inverse-gamma_distribution
Beispiele
Angenommen, wir möchten den Zusammenhang zwischen der Normal-Invers-Gamma-Verteilung und der Invers-Gamma-Verteilung untersuchen.
>>> import numpy as np >>> from scipy import stats >>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng() >>> mu, lmbda, a, b = 0, 1, 20, 20 >>> norm_inv_gamma = stats.normal_inverse_gamma(mu, lmbda, a, b) >>> inv_gamma = stats.invgamma(a, scale=b)
Ein Ansatz ist, die Verteilung der s2-Elemente von Zufallsvariablen mit der PDF einer Invers-Gamma-Verteilung zu vergleichen.
>>> _, s2 = norm_inv_gamma.rvs(size=10000, random_state=rng) >>> bins = np.linspace(s2.min(), s2.max(), 50) >>> plt.hist(s2, bins=bins, density=True, label='Frequency density') >>> s2 = np.linspace(s2.min(), s2.max(), 300) >>> plt.plot(s2, inv_gamma.pdf(s2), label='PDF') >>> plt.xlabel(r'$\sigma^2$') >>> plt.ylabel('Frequency density / PMF') >>> plt.show()
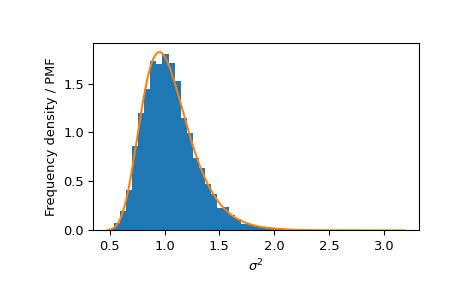
Ebenso können wir die marginale Verteilung von s2 mit einer Invers-Gamma-Verteilung vergleichen.
>>> from scipy.integrate import quad_vec >>> from scipy import integrate >>> s2 = np.linspace(0.5, 3, 6) >>> res = quad_vec(lambda x: norm_inv_gamma.pdf(x, s2), -np.inf, np.inf)[0] >>> np.allclose(res, inv_gamma.pdf(s2)) True
Der Stichprobenmittelwert ist mit dem Mittelwert der Verteilung vergleichbar.
>>> x, s2 = norm_inv_gamma.rvs(size=10000, random_state=rng) >>> x.mean(), s2.mean() (np.float64(-0.005254750127304425), np.float64(1.050438111436508)) >>> norm_inv_gamma.mean() (np.float64(0.0), np.float64(1.0526315789473684))
Ähnlich gilt für die Varianz
>>> x.var(ddof=1), s2.var(ddof=1) (np.float64(1.0546150578185023), np.float64(0.061829865266330754)) >>> norm_inv_gamma.var() (np.float64(1.0526315789473684), np.float64(0.061557402277623886))