rv_discrete#
- class scipy.stats.rv_discrete(a=0, b=inf, name=None, badvalue=None, moment_tol=1e-08, values=None, inc=1, longname=None, shapes=None, seed=None)[Quelle]#
Eine generische diskrete Zufallsvariablenklasse zur Unterklassifizierung.
rv_discreteist eine Basisklasse zur Erstellung spezifischer Verteilungsklassen und -instanzen für diskrete Zufallsvariablen. Sie kann auch zur Erstellung einer beliebigen Verteilung verwendet werden, die durch eine Liste von Stützpunkten und entsprechenden Wahrscheinlichkeiten definiert ist.- Parameter:
- afloat, optional
Untere Schranke des Trägers der Verteilung, Standard: 0
- bfloat, optional
Obere Schranke des Trägers der Verteilung, Standard: plus unendlich
- moment_tolfloat, optional
Die Toleranz für die allgemeine Berechnung von Momenten.
- valuestuple aus zwei Array_likes, optional
(xk, pk)wobeixkganze Zahlen sind undpkdie von Null verschiedenen Wahrscheinlichkeiten zwischen 0 und 1 sind, mitsum(pk) = 1.xkundpkmüssen die gleiche Form haben, undxkmuss eindeutig sein.- incinteger, optional
Schrittweite für den Träger der Verteilung. Standard ist 1. (andere Werte wurden nicht getestet)
- badvaluefloat, optional
Der Wert in Ergebnis-Arrays, der einen Wert angibt, für den eine Argumentbeschränkung verletzt ist, Standard ist np.nan.
- namestr, optional
Der Name der Instanz. Diese Zeichenkette wird verwendet, um das Standardbeispiel für Verteilungen zu erstellen.
- longnamestr, optional
Diese Zeichenkette wird als Teil der ersten Zeile des Docstrings verwendet, der zurückgegeben wird, wenn eine Unterklasse keinen eigenen Docstring hat. Hinweis: longname existiert aus Kompatibilitätsgründen, verwenden Sie es nicht für neue Unterklassen.
- shapesstr, optional
Die Form der Verteilung. Zum Beispiel "m, n" für eine Verteilung, die zwei Ganzzahlen als die beiden Formargumente für alle ihre Methoden entgegennimmt. Wenn nicht angegeben, werden die Formparameter aus den Signaturen der privaten Methoden,
_pmfund_cdfder Instanz, abgeleitet.- seed{None, int,
numpy.random.Generator,numpy.random.RandomState}, optional Wenn seed None ist (oder np.random), wird die Singleton-Instanz von
numpy.random.RandomStateverwendet. Wenn seed eine Ganzzahl ist, wird eine neueRandomState-Instanz mit seed initialisiert. Wenn seed bereits eineGenerator- oderRandomState-Instanz ist, wird diese Instanz verwendet.
- Attribute:
- a, bfloat, optional
Untere/obere Schranke des Trägers der unverschobenen/unskalierten Verteilung. Dieser Wert wird von den Parametern loc und scale nicht beeinflusst. Um den Träger der verschobenen/skalierten Verteilung zu berechnen, verwenden Sie die Methode
support.
Methoden
rvs(*args, **kwargs)Zufallsvariablen des angegebenen Typs.
pmf(k, *args, **kwds)Wahrscheinlichkeitsmassenfunktion an der Stelle k der gegebenen RV.
logpmf(k, *args, **kwds)Logarithmus der Wahrscheinlichkeitsmassenfunktion an der Stelle k der gegebenen RV.
cdf(k, *args, **kwds)Kumulative Verteilungsfunktion (CDF) der gegebenen RV.
logcdf(k, *args, **kwds)Logarithmus der kumulativen Verteilungsfunktion an der Stelle k der gegebenen RV.
sf(k, *args, **kwds)Überlebensfunktion (1 -
cdf) an der Stelle k der gegebenen RV.logsf(k, *args, **kwds)Logarithmus der Überlebensfunktion der gegebenen RV.
ppf(q, *args, **kwds)Perzentilpunktfunktion (Umkehrung von
cdf) an der Stelle q der gegebenen RV.isf(q, *args, **kwds)Umgekehrte Überlebensfunktion (Umkehrung von
sf) an der Stelle q der gegebenen RV.moment(order, *args, **kwds)nicht-zentrales Moment der Verteilung der angegebenen Ordnung.
stats(*args, **kwds)Einige Statistiken der gegebenen RV.
entropy(*args, **kwds)Differenzielle Entropie der RV.
expect([func, args, loc, lb, ub, ...])Erwartungswert einer Funktion bezüglich der Verteilung für diskrete Verteilung durch numerische Summierung berechnen.
median(*args, **kwds)Median der Verteilung.
mean(*args, **kwds)Mittelwert der Verteilung.
std(*args, **kwds)Standardabweichung der Verteilung.
var(*args, **kwds)Varianz der Verteilung.
interval(confidence, *args, **kwds)Konfidenzintervall mit gleichen Flächen um den Median.
__call__(*args, **kwds)Fixiert die Verteilung für die gegebenen Argumente.
support(*args, **kwargs)Unterstützung der Verteilung.
Hinweise
Diese Klasse ist ähnlich wie
rv_continuous. Ob ein Formparameter gültig ist, wird durch eine_argcheckMethode entschieden (die standardmäßig prüft, ob ihre Argumente strikt positiv sind). Die Hauptunterschiede sind wie folgt.Der Träger der Verteilung ist eine Menge von ganzen Zahlen.
Anstelle der Wahrscheinlichkeitsdichtefunktion,
pdf(und die entsprechende private_pdf), definiert diese Klasse die *Wahrscheinlichkeitsmassenfunktion*pmf(und die entsprechende private_pmf).Es gibt keinen
scaleParameter.Die Standardimplementierungen von Methoden (z.B.
_cdf) sind nicht für Verteilungen mit einem nach unten unbeschränkten Träger (d.h.a=-np.inf) ausgelegt, daher müssen sie überschrieben werden.
Um eine neue diskrete Verteilung zu erstellen, würden wir Folgendes tun
>>> from scipy.stats import rv_discrete >>> class poisson_gen(rv_discrete): ... "Poisson distribution" ... def _pmf(self, k, mu): ... return exp(-mu) * mu**k / factorial(k)
und eine Instanz erstellen
>>> poisson = poisson_gen(name="poisson")
Beachten Sie, dass wir oben die Poisson-Verteilung in der Standardform definiert haben. Das Verschieben der Verteilung kann durch Angabe des Parameters
locfür die Methoden der Instanz erfolgen. Zum Beispiel delegiertpoisson.pmf(x, mu, loc)die Arbeit anpoisson._pmf(x-loc, mu).Diskrete Verteilungen aus einer Liste von Wahrscheinlichkeiten
Alternativ können Sie eine beliebige diskrete RV konstruieren, die auf einer endlichen Menge von Werten
xkmitProb{X=xk} = pkdefiniert ist, indem Sie das Schlüsselwortargumentvaluesfür den Konstruktorrv_discreteverwenden.Deepcopying / Pickling
Wenn eine Verteilung oder eine gefrorene Verteilung deepgecopyt (gepickelt/entpickelt etc.) wird, wird jeder zugrunde liegende Zufallszahlengenerator mitkopiert. Eine Folge davon ist, dass, wenn eine Verteilung vor dem Kopieren auf dem Singleton-Zustand RandomState basiert, sie nach dem Kopieren auf einer Kopie dieses Zufallszustands basiert, und
np.random.seedden Zustand nicht mehr kontrolliert.Beispiele
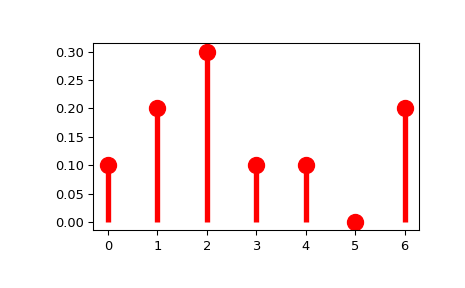
Benutzerdefinierte diskrete Verteilung
>>> import numpy as np >>> from scipy import stats >>> xk = np.arange(7) >>> pk = (0.1, 0.2, 0.3, 0.1, 0.1, 0.0, 0.2) >>> custm = stats.rv_discrete(name='custm', values=(xk, pk)) >>> >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1) >>> ax.plot(xk, custm.pmf(xk), 'ro', ms=12, mec='r') >>> ax.vlines(xk, 0, custm.pmf(xk), colors='r', lw=4) >>> plt.show()
Zufallszahlengenerierung
>>> R = custm.rvs(size=100)