scipy.stats.vonmises_fisher#

scipy.stats.vonmises_fisher = <scipy.stats._multivariate.vonmises_fisher_gen object>[Quelle]#

Eine von Mises-Fisher-Variable.

Das Schlüsselwort mu gibt den mittleren Richtungsvektor an. Das Schlüsselwort kappa gibt den Konzentrationsparameter an.

Parameter:

muarray_like: Mittlere Richtung der Verteilung. Muss ein eindimensionaler Einheitsvektor der Norm 1 sein.
kappafloat: Konzentrationsparameter. Muss positiv sein.
seed{None, int, np.random.RandomState, np.random.Generator}, optional: Wird zum Ziehen von Zufallsvarianten verwendet. Wenn seed None ist, wird die RandomState Singleton verwendet. Wenn seed eine Ganzzahl ist, wird eine neue RandomState-Instanz verwendet, die mit seed initialisiert wird. Wenn seed bereits eine RandomState- oder Generator-Instanz ist, wird dieses Objekt verwendet. Standard ist None.

Methoden

pdf(x, mu=None, kappa=1)	Wahrscheinlichkeitsdichtefunktion.
logpdf(x, mu=None, kappa=1)	Logarithmus der Wahrscheinlichkeitsdichtefunktion.
rvs(mu=None, kappa=1, size=1, random_state=None)	Zufällige Stichproben aus einer von Mises-Fisher-Verteilung ziehen.
entropy(mu=None, kappa=1)	Berechnet die differentielle Entropie der von Mises-Fisher-Verteilung.
fit(data)	Passt eine von Mises-Fisher-Verteilung an Daten an.

Siehe auch

scipy.stats.vonmises: Von-Mises-Fisher-Verteilung in 2D auf einem Kreis
uniform_direction: Gleichverteilung auf der Oberfläche einer Hypersphäre

Hinweise

Die von Mises-Fisher-Verteilung ist eine gerichtete Verteilung auf der Oberfläche der Einheits-Hypersphäre. Die Wahrscheinlichkeitsdichtefunktion eines Einheitsvektors \(\mathbf{x}\) ist

\[f(\mathbf{x}) = \frac{\kappa^{d/2-1}}{(2\pi)^{d/2}I_{d/2-1}(\kappa)} \exp\left(\kappa \mathbf{\mu}^T\mathbf{x}\right),\]

wobei \(\mathbf{\mu}\) die mittlere Richtung, \(\kappa\) der Konzentrationsparameter, \(d\) die Dimension und \(I\) die modifizierte Bessel-Funktion erster Art sind. Da \(\mu\) eine Richtung darstellt, muss es ein Einheitsvektor sein oder anders ausgedrückt, ein Punkt auf der Hypersphäre: \(\mathbf{\mu}\in S^{d-1}\). \(\kappa\) ist ein Konzentrationsparameter, was bedeutet, dass er positiv sein muss (\(\kappa>0\)) und dass die Verteilung bei zunehmendem \(\kappa\) enger wird. In diesem Sinne ähnelt der Kehrwert \(1/\kappa\) dem Varianzparameter der Normalverteilung.

Die von Mises-Fisher-Verteilung dient oft als Analogon zur Normalverteilung auf der Sphäre. Intuitiv ist für Einheitsvektoren ein nützliches Maß für den Abstand der Winkel \(\alpha\) zwischen ihnen. Dies ist genau das, was das Skalarprodukt \(\mathbf{\mu}^T\mathbf{x}=\cos(\alpha)\) in der von Mises-Fisher-Wahrscheinlichkeitsdichtefunktion beschreibt: der Winkel zwischen der mittleren Richtung \(\mathbf{\mu}\) und dem Vektor \(\mathbf{x}\). Je größer der Winkel zwischen ihnen, desto geringer ist die Wahrscheinlichkeit, \(\mathbf{x}\) für diese spezielle mittlere Richtung \(\mathbf{\mu}\) zu beobachten.

In den Dimensionen 2 und 3 werden spezialisierte Algorithmen für schnelles Sampling verwendet [2], [3]. Für Dimensionen von 4 oder höher wird der in [4] beschriebene Abwerbungsalgorithmus verwendet. Diese Implementierung basiert teilweise auf dem geomstats-Paket [5], [6].

Hinzugefügt in Version 1.11.

Referenzen

[1]

Von Mises-Fisher-Verteilung, Wikipedia, https://en.wikipedia.org/wiki/Von_Mises%E2%80%93Fisher_distribution

[2]

Mardia, K. und Jupp, P. Directional statistics. Wiley, 2000.

[3]

J. Wenzel. Numerisch stabile Stichprobennahme aus der von Mises Fisher-Verteilung auf S2. https://www.mitsuba-renderer.org/~wenzel/files/vmf.pdf

[4]

Wood, A. Simulation of the von mises fisher distribution. Communications in statistics-simulation and computation 23, 1 (1994), 157-164. https://doi.org/10.1080/03610919408813161

[5]

geomstats, Github. MIT-Lizenz. Zugriffsdatum: 06.01.2023. geomstats/geomstats

[6]

Miolane, N. et al. Geomstats: Ein Python-Paket für Riemannsche Geometrie im maschinellen Lernen. Journal of Machine Learning Research 21 (2020). http://jmlr.org/papers/v21/19-027.html

Beispiele

Visualisierung der Wahrscheinlichkeitsdichte

Zeichnen Sie die Wahrscheinlichkeitsdichte in drei Dimensionen für steigenden Konzentrationsparameter. Die Dichte wird mit der Methode pdf berechnet.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import vonmises_fisher
>>> from matplotlib.colors import Normalize
>>> n_grid = 100
>>> u = np.linspace(0, np.pi, n_grid)
>>> v = np.linspace(0, 2 * np.pi, n_grid)
>>> u_grid, v_grid = np.meshgrid(u, v)
>>> vertices = np.stack([np.cos(v_grid) * np.sin(u_grid),
...                      np.sin(v_grid) * np.sin(u_grid),
...                      np.cos(u_grid)],
...                     axis=2)
>>> x = np.outer(np.cos(v), np.sin(u))
>>> y = np.outer(np.sin(v), np.sin(u))
>>> z = np.outer(np.ones_like(u), np.cos(u))
>>> def plot_vmf_density(ax, x, y, z, vertices, mu, kappa):
...     vmf = vonmises_fisher(mu, kappa)
...     pdf_values = vmf.pdf(vertices)
...     pdfnorm = Normalize(vmin=pdf_values.min(), vmax=pdf_values.max())
...     ax.plot_surface(x, y, z, rstride=1, cstride=1,
...                     facecolors=plt.cm.viridis(pdfnorm(pdf_values)),
...                     linewidth=0)
...     ax.set_aspect('equal')
...     ax.view_init(azim=-130, elev=0)
...     ax.axis('off')
...     ax.set_title(rf"$\kappa={kappa}$")
>>> fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(9, 4),
...                          subplot_kw={"projection": "3d"})
>>> left, middle, right = axes
>>> mu = np.array([-np.sqrt(0.5), -np.sqrt(0.5), 0])
>>> plot_vmf_density(left, x, y, z, vertices, mu, 5)
>>> plot_vmf_density(middle, x, y, z, vertices, mu, 20)
>>> plot_vmf_density(right, x, y, z, vertices, mu, 100)
>>> plt.subplots_adjust(top=1, bottom=0.0, left=0.0, right=1.0, wspace=0.)
>>> plt.show()

../../_images/scipy-stats-vonmises_fisher-1_00_00.png

Wenn wir den Konzentrationsparameter erhöhen, werden die Punkte stärker um die mittlere Richtung gruppiert.

Sampling

Ziehen Sie 5 Stichproben aus der Verteilung mit der Methode rvs, was zu einem 5x3-Array führt.

>>> rng = np.random.default_rng()
>>> mu = np.array([0, 0, 1])
>>> samples = vonmises_fisher(mu, 20).rvs(5, random_state=rng)
>>> samples
array([[ 0.3884594 , -0.32482588,  0.86231516],
       [ 0.00611366, -0.09878289,  0.99509023],
       [-0.04154772, -0.01637135,  0.99900239],
       [-0.14613735,  0.12553507,  0.98126695],
       [-0.04429884, -0.23474054,  0.97104814]])

Diese Stichproben sind Einheitsvektoren auf der Sphäre \(S^2\). Zur Überprüfung berechnen wir ihre euklidischen Normen

>>> np.linalg.norm(samples, axis=1)
array([1., 1., 1., 1., 1.])

Zeichnen Sie 20 Beobachtungen, die aus der von Mises-Fisher-Verteilung für steigenden Konzentrationsparameter \(\kappa\) gezogen wurden. Der rote Punkt hebt die mittlere Richtung \(\mu\) hervor.

>>> def plot_vmf_samples(ax, x, y, z, mu, kappa):
...     vmf = vonmises_fisher(mu, kappa)
...     samples = vmf.rvs(20)
...     ax.plot_surface(x, y, z, rstride=1, cstride=1, linewidth=0,
...                     alpha=0.2)
...     ax.scatter(samples[:, 0], samples[:, 1], samples[:, 2], c='k', s=5)
...     ax.scatter(mu[0], mu[1], mu[2], c='r', s=30)
...     ax.set_aspect('equal')
...     ax.view_init(azim=-130, elev=0)
...     ax.axis('off')
...     ax.set_title(rf"$\kappa={kappa}$")
>>> mu = np.array([-np.sqrt(0.5), -np.sqrt(0.5), 0])
>>> fig, axes = plt.subplots(nrows=1, ncols=3,
...                          subplot_kw={"projection": "3d"},
...                          figsize=(9, 4))
>>> left, middle, right = axes
>>> plot_vmf_samples(left, x, y, z, mu, 5)
>>> plot_vmf_samples(middle, x, y, z, mu, 20)
>>> plot_vmf_samples(right, x, y, z, mu, 100)
>>> plt.subplots_adjust(top=1, bottom=0.0, left=0.0,
...                     right=1.0, wspace=0.)
>>> plt.show()

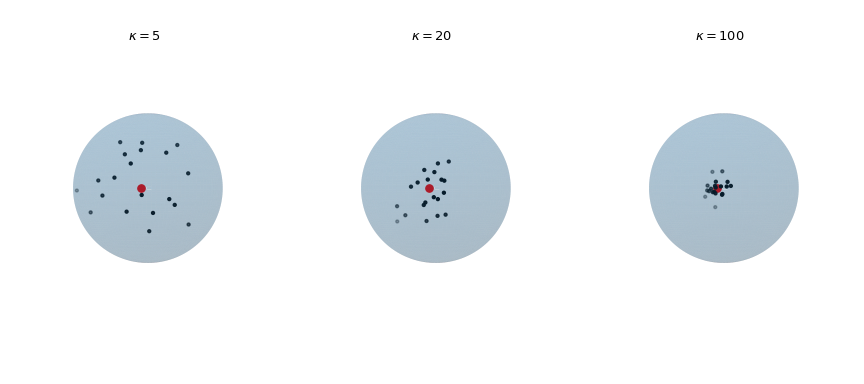
../../_images/scipy-stats-vonmises_fisher-1_01_00.png

Die Diagramme zeigen, dass mit zunehmender Konzentration \(\kappa\) die resultierenden Stichproben enger um die mittlere Richtung zentriert sind.

Anpassen der Verteilungsparameter

Die Verteilung kann mithilfe der Methode fit an Daten angepasst werden, die die geschätzten Parameter zurückgibt. Als Spielbeispiel passen wir die Verteilung an Stichproben an, die aus einer bekannten von Mises-Fisher-Verteilung gezogen wurden.

>>> mu, kappa = np.array([0, 0, 1]), 20
>>> samples = vonmises_fisher(mu, kappa).rvs(1000, random_state=rng)
>>> mu_fit, kappa_fit = vonmises_fisher.fit(samples)
>>> mu_fit, kappa_fit
(array([0.01126519, 0.01044501, 0.99988199]), 19.306398751730995)

Wir sehen, dass die geschätzten Parameter mu_fit und kappa_fit sehr nahe an den tatsächlichen Parametern liegen.