scipy.signal.windows.

bartlett

scipy.signal.windows.bartlett(M, sym=True, *, xp=None, device=None)

Gibt ein Bartlett-Fenster zurück.

Das Bartlett-Fenster ist dem dreieckigen Fenster sehr ähnlich, mit dem Unterschied, dass die Endpunkte bei Null liegen. Es wird oft in der Signalverarbeitung verwendet, um ein Signal abzutasten, ohne zu viel Rauschen im Frequenzbereich zu erzeugen.

Parameter:

Mint

Anzahl der Punkte im Ausgabefenster. Wenn Null, wird ein leeres Array zurückgegeben. Bei negativen Werten wird eine Ausnahme ausgelöst.

symbool, optional

Wenn True (Standard), wird ein symmetrisches Fenster zur Filterentwurf verwendet. Wenn False, wird ein periodisches Fenster für die Spektralanalyse generiert.

xparray_namespace, optional

Optionaler Array-Namespace. Sollte mit dem Array-API-Standard kompatibel sein oder von array-api-compat unterstützt werden. Standard: numpy

device: any

optionale Gerätespezifikation für die Ausgabe. Sollte mit einer der unterstützten Gerätespezifikationen in xp übereinstimmen.

Rückgabe:

wndarray

Das dreieckige Fenster mit den ersten und letzten Abtastwerten gleich Null und dem Maximalwert auf 1 normiert (obwohl der Wert 1 nicht erscheint, wenn M gerade und sym True ist).

Siehe auch

triang

Ein dreieckiges Fenster, das die Null an den Enden nicht berührt

Hinweise

Das Bartlett-Fenster ist definiert als

\[w(n) = \frac{2}{M-1} \left( \frac{M-1}{2} - \left|n - \frac{M-1}{2}\right| \right)\]

Die meisten Referenzen zum Bartlett-Fenster stammen aus der Literatur zur Signalverarbeitung, wo es als eine von vielen Fensterfunktionen zur Glättung von Werten verwendet wird. Beachten Sie, dass die Faltung mit diesem Fenster eine lineare Interpolation ergibt. Es ist auch als Apodisationsfunktion (die "Entfernung des Fußes" bedeutet, d. h. Glättung von Diskontinuitäten am Anfang und Ende des abgetasteten Signals) oder als Abschwächungsfunktion bekannt. Die Fourier-Transformation des Bartlett ist das Produkt zweier Sinc-Funktionen. Beachten Sie die ausgezeichnete Diskussion in Kanasewich. [2]

Referenzen

[1]

M.S. Bartlett, „Periodogram Analysis and Continuous Spectra“, Biometrika 37, 1-16, 1950.

[2]

E.R. Kanasewich, „Time Sequence Analysis in Geophysics“, The University of Alberta Press, 1975, S. 109-110.

[3]

A.V. Oppenheim und R.W. Schafer, „Discrete-Time Signal Processing“, Prentice-Hall, 1999, S. 468-471.

[4]

Wikipedia, „Fensterfunktion“, https://en.wikipedia.org/wiki/Window_function

[5]

W.H. Press, B.P. Flannery, S.A. Teukolsky und W.T. Vetterling, „Numerical Recipes“, Cambridge University Press, 1986, Seite 429.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Plotten Sie das Fenster und seine Frequenzantwort

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

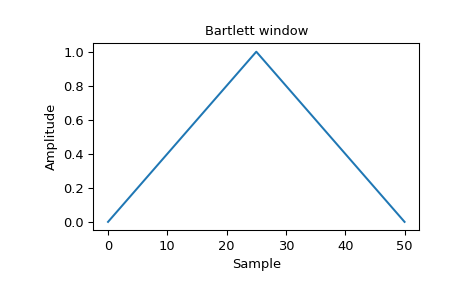
>>> window = signal.windows.bartlett(51)
>>> plt.plot(window)
>>> plt.title("Bartlett window")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

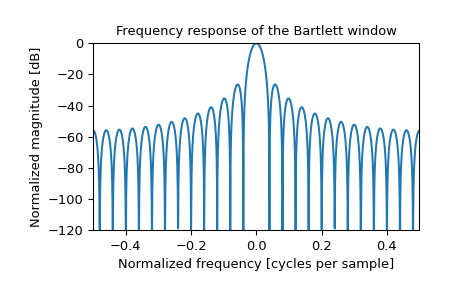
>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -120, 0])
>>> plt.title("Frequency response of the Bartlett window")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")

ZurückIn Tab öffnen