scipy.signal.windows.

chebwin

scipy.signal.windows.chebwin(M, at, sym=True, *, xp=None, device=None)

Gibt ein Dolph-Chebyshev-Fenster zurück.

Parameter:

Mint

Anzahl der Punkte im Ausgabefenster. Wenn Null, wird ein leeres Array zurückgegeben. Bei negativen Werten wird eine Ausnahme ausgelöst.

atfloat

Dämpfung (in dB).

symbool, optional

Wenn True (Standard), wird ein symmetrisches Fenster zur Filterentwurf verwendet. Wenn False, wird ein periodisches Fenster für die Spektralanalyse generiert.

xparray_namespace, optional

Optionaler Array-Namespace. Sollte mit dem Array-API-Standard kompatibel sein oder von array-api-compat unterstützt werden. Standard: numpy

device: any

optionale Gerätespezifikation für die Ausgabe. Sollte mit einer der unterstützten Gerätespezifikationen in xp übereinstimmen.

Rückgabe:

wndarray

Das Fenster, dessen Maximalwert immer auf 1 normiert ist.

Hinweise

Dieses Fenster optimiert die schmalste Hauptkeulenbreite für eine gegebene Ordnung M und eine Nebenkeulendämpfung at mittels Tschebyscheff-Polynomen. Es wurde ursprünglich von Dolph entwickelt, um die Richtwirkung von Funkantennenarrays zu optimieren.

Im Gegensatz zu den meisten Fenstern wird das Dolph-Chebyshev-Fenster über seine Frequenzantwort definiert

\[W(k) = \frac {\cos\{M \cos^{-1}[\beta \cos(\frac{\pi k}{M})]\}} {\cosh[M \cosh^{-1}(\beta)]}\]

wo

\[\beta = \cosh \left [\frac{1}{M} \cosh^{-1}(10^\frac{A}{20}) \right ]\]

und 0 <= abs(k) <= M-1. A ist die Dämpfung in Dezibel (at).

Das Zeitbereichsfenster wird dann mittels der IFFT erzeugt, daher sind Potenzen von zwei für M am schnellsten zu generieren und Primzahlen für M am langsamsten.

Die Gleichwelligkeitsbedingung im Frequenzbereich erzeugt Impulse im Zeitbereich, die an den Enden des Fensters erscheinen.

Referenzen

[1]

C. Dolph, "A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level", Proceedings of the IEEE, Vol. 34, Issue 6

[2]

Peter Lynch, "The Dolph-Chebyshev Window: A Simple Optimal Filter", American Meteorological Society (April 1997) http://mathsci.ucd.ie/~plynch/Publications/Dolph.pdf

[3]

F. J. Harris, "On the use of windows for harmonic analysis with the discrete Fourier transforms", Proceedings of the IEEE, Vol. 66, No. 1, January 1978

Beispiele

Probieren Sie es in Ihrem Browser aus!

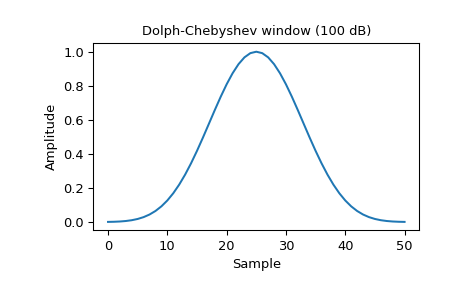
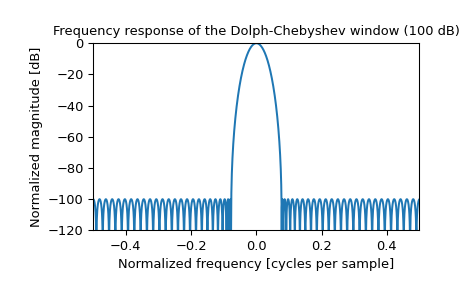
Plotten Sie das Fenster und seine Frequenzantwort

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = signal.windows.chebwin(51, at=100)
>>> plt.plot(window)
>>> plt.title("Dolph-Chebyshev window (100 dB)")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -120, 0])
>>> plt.title("Frequency response of the Dolph-Chebyshev window (100 dB)")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")

ZurückIn Tab öffnen