scipy.signal.windows.

general_cosine

scipy.signal.windows.general_cosine(M, a, sym=True)

Generisches gewichtetes Summen von Kosinustermen Fenster

Parameter:

Mint

Anzahl der Punkte im Ausgabe-Fenster

aarray_like

Sequenz von Gewichtungskoeffizienten. Dies folgt der Konvention, auf den Ursprung zentriert zu sein, daher werden dies typischerweise alles positive Zahlen sein, nicht abwechselnd im Vorzeichen.

symbool, optional

Wenn True (Standard), wird ein symmetrisches Fenster zur Filterentwurf verwendet. Wenn False, wird ein periodisches Fenster für die Spektralanalyse generiert.

Rückgabe:

wndarray

Das Array der Fensterwerte.

Referenzen

[1]

A. Nuttall, „Some windows with very good sidelobe behavior,“ IEEE Transactions on Acoustics, Speech, and Signal Processing, Bd. 29, Nr. 1, S. 84-91, Feb 1981. DOI:10.1109/TASSP.1981.1163506.

[2]

Heinzel G. et al., „Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new flat-top windows“, 15. Februar 2002 https://holometer.fnal.gov/GH_FFT.pdf

Beispiele

Probieren Sie es in Ihrem Browser aus!

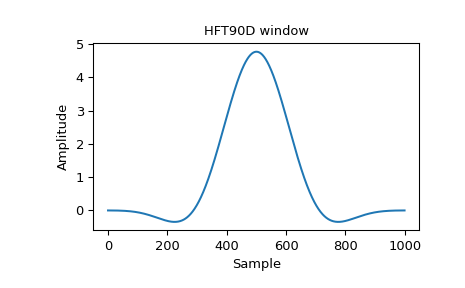
Heinzel beschreibt ein Flat-Top-Fenster namens „HFT90D“ mit der Formel: [2]

\[w_j = 1 - 1.942604 \cos(z) + 1.340318 \cos(2z) - 0.440811 \cos(3z) + 0.043097 \cos(4z)\]

wo

\[z = \frac{2 \pi j}{N}, j = 0...N - 1\]

Da dies die Konvention verwendet, am Ursprung zu beginnen, müssen wir zur Reproduktion des Fensters jeden zweiten Koeffizienten in eine positive Zahl umwandeln

>>> HFT90D = [1, 1.942604, 1.340318, 0.440811, 0.043097]

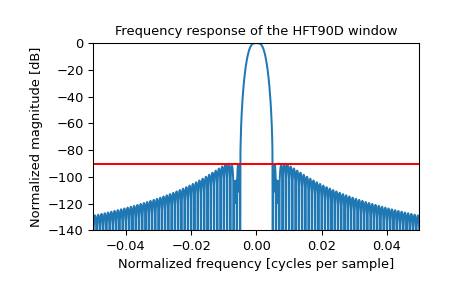
Das Paper besagt, dass die höchste Seitenkeule bei -90,2 dB liegt. Reproduzieren Sie Abbildung 42, indem Sie das Fenster und seine Frequenzantwort plotten, und bestätigen Sie die Seitenkeulenpegel in Rot

>>> import numpy as np
>>> from scipy.signal.windows import general_cosine
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = general_cosine(1000, HFT90D, sym=False)
>>> plt.plot(window)
>>> plt.title("HFT90D window")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

>>> plt.figure()
>>> A = fft(window, 10000) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = np.abs(fftshift(A / abs(A).max()))
>>> response = 20 * np.log10(np.maximum(response, 1e-10))
>>> plt.plot(freq, response)
>>> plt.axis([-50/1000, 50/1000, -140, 0])
>>> plt.title("Frequency response of the HFT90D window")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")
>>> plt.axhline(-90.2, color='red')
>>> plt.show()

ZurückIn Tab öffnen