scipy.integrate.

solve_ivp#

scipy.integrate.solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, dense_output=False, events=None, vectorized=False, args=None, **options)[Quelle]#

Löst ein Anfangswertproblem für ein System von ODEs.

Diese Funktion integriert numerisch ein System von gewöhnlichen Differentialgleichungen, gegeben einen Anfangswert.

dy / dt = f(t, y)
y(t0) = y0

Hier ist t eine 1-dimensionale unabhängige Variable (Zeit), y(t) ist eine N-dimensionale vektorwertige Funktion (Zustand) und eine N-dimensionale vektorwertige Funktion f(t, y) bestimmt die Differentialgleichungen. Das Ziel ist, y(t) approximativ zu finden, das die Differentialgleichungen erfüllt, gegeben einen Anfangswert y(t0)=y0.

Einige der Löser unterstützen die Integration im komplexen Bereich, aber beachten Sie, dass für steife ODE-Löser die rechte Seite komplex differenzierbar sein muss (Cauchy-Riemann-Gleichungen erfüllen [11]). Um ein Problem im komplexen Bereich zu lösen, übergeben Sie y0 mit einem komplexen Datentyp. Eine andere immer verfügbare Option ist, Ihr Problem separat für Real- und Imaginärteil umzuschreiben.

Parameter:

funcallable

Rechte Seite des Systems: die Zeitableitung des Zustands y zum Zeitpunkt t. Die Aufrufsignatur ist fun(t, y), wobei t ein Skalar und y ein ndarray mit len(y) = len(y0) ist. Zusätzliche Argumente müssen übergeben werden, wenn args verwendet wird (siehe Dokumentation des Arguments args). fun muss ein Array der gleichen Form wie y zurückgeben. Siehe vectorized für weitere Informationen.

t_span2-element Sequenz

Integrationsintervall (t0, tf). Der Löser startet mit t=t0 und integriert, bis er t=tf erreicht. Sowohl t0 als auch tf müssen Floats oder Werte sein, die von der Float-Konvertierungsfunktion interpretierbar sind.

y0array_like, shape (n,)

Anfangszustand. Für Probleme im komplexen Bereich übergeben Sie y0 mit einem komplexen Datentyp (auch wenn der Anfangswert rein reell ist).

methodString oder OdeSolver, optional

Verwendete Integrationsmethode

‘RK45’ (Standard): Explizite Runge-Kutta-Methode der Ordnung 5(4) [1]. Der Fehler wird unter der Annahme der Genauigkeit der Methode vierter Ordnung kontrolliert, aber Schritte werden unter Verwendung der Formel fünfter Ordnung (lokale Extrapolation wird durchgeführt) unternommen. Ein quartisches Interpolationspolynom wird für die dichte Ausgabe verwendet [2]. Kann im komplexen Bereich angewendet werden.

‘RK23’: Explizite Runge-Kutta-Methode der Ordnung 3(2) [3]. Der Fehler wird unter der Annahme der Genauigkeit der Methode zweiter Ordnung kontrolliert, aber Schritte werden unter Verwendung der Formel dritter Ordnung (lokale Extrapolation wird durchgeführt) unternommen. Ein kubisches Hermite-Polynom wird für die dichte Ausgabe verwendet. Kann im komplexen Bereich angewendet werden.

‘DOP853’: Explizite Runge-Kutta-Methode der Ordnung 8 [13]. Python-Implementierung des Algorithmus „DOP853“, ursprünglich in Fortran geschrieben [14]. Ein Interpolationspolynom 7. Ordnung mit Genauigkeit 7. Ordnung wird für die dichte Ausgabe verwendet. Kann im komplexen Bereich angewendet werden.

‘Radau’: Implizite Runge-Kutta-Methode der Radau IIA-Familie der Ordnung 5 [4]. Der Fehler wird mit einer Formel dritter Ordnung gesteuert. Ein kubisches Polynom, das die Kollokationsbedingungen erfüllt, wird für die dichte Ausgabe verwendet.

‘BDF’: Implizite Mehrschrittmethode variabler Ordnung (1 bis 5) basierend auf einer Backward-Differentiation-Formel zur Approximation der Ableitung [5]. Die Implementierung folgt der in [6] beschriebenen. Ein quasi-konstantes Schrittweitenverfahren wird verwendet und die Genauigkeit wird durch die NDF-Modifikation erhöht. Kann im komplexen Bereich angewendet werden.

‘LSODA’: Adams/BDF-Methode mit automatischer Steifigkeitserkennung und -umschaltung [7], [8]. Dies ist ein Wrapper für den Fortran-Löser von ODEPACK.

Explizite Runge-Kutta-Methoden (‘RK23’, ‘RK45’, ‘DOP853’) sollten für nicht-steife Probleme verwendet werden und implizite Methoden (‘Radau’, ‘BDF’) für steife Probleme [9]. Unter den Runge-Kutta-Methoden wird ‘DOP853’ für die Lösung mit hoher Präzision (niedrige Werte von rtol und atol) empfohlen.

Wenn Sie unsicher sind, versuchen Sie zuerst, ‘RK45’ auszuführen. Wenn es ungewöhnlich viele Iterationen benötigt, divergiert oder fehlschlägt, ist Ihr Problem wahrscheinlich steif und Sie sollten ‘Radau’ oder ‘BDF’ verwenden. ‘LSODA’ kann auch eine gute universelle Wahl sein, aber es könnte etwas umständlicher zu handhaben sein, da es alte Fortran-Codes umschließt.

Sie können auch eine beliebige Klasse übergeben, die von OdeSolver abgeleitet ist und den Löser implementiert.

t_evalArray-ähnlich oder None, optional

Zeitpunkte, an denen die berechnete Lösung gespeichert werden soll; müssen sortiert sein und innerhalb von t_span liegen. Wenn None (Standard), werden Punkte verwendet, die vom Löser ausgewählt wurden.

dense_outputBool, optional

Ob eine kontinuierliche Lösung berechnet werden soll. Standard ist False.

eventsAufrufbar oder Liste von Aufrufbaren, optional

Zu verfolgende Ereignisse. Wenn None (Standard), werden keine Ereignisse verfolgt. Jedes Ereignis tritt an den Nullstellen einer kontinuierlichen Funktion von Zeit und Zustand auf. Jede Funktion muss die Signatur event(t, y) haben, wobei zusätzliche Argumente übergeben werden müssen, wenn args verwendet wird (siehe Dokumentation des Arguments args). Jede Funktion muss einen Float zurückgeben. Der Löser findet einen genauen Wert von t, an dem event(t, y(t)) = 0 gilt, unter Verwendung eines Wurzel-Findungsalgorithmus. Standardmäßig werden alle Nullstellen gefunden. Der Löser sucht nach einem Vorzeichenwechsel über jeden Schritt, sodass, wenn mehrere Nullstellenübergänge innerhalb eines Schritts auftreten, Ereignisse möglicherweise übersehen werden. Zusätzlich kann jede event-Funktion die folgenden Attribute haben

terminal: Bool oder Int, optional
Wenn boolesch, ob die Integration abgebrochen werden soll, wenn dieses Ereignis eintritt. Wenn integral, tritt die Beendigung nach der angegebenen Anzahl von Ereignissen dieses Typs ein. Standardmäßig False, wenn nicht zugewiesen.

direction: Float, optional
Richtung eines Nullstellenübergangs. Wenn direction positiv ist, wird event nur ausgelöst, wenn von negativ nach positiv gegangen wird, und umgekehrt, wenn direction negativ ist. Wenn 0, dann löst jede Richtung das Ereignis aus. Standardmäßig 0, wenn nicht zugewiesen.

Sie können Attribute wie event.terminal = True jeder Funktion in Python zuweisen.

vectorizedbool, optional

Ob fun vektorisiert aufgerufen werden kann. Standard ist False.

Wenn vectorized False ist, wird fun immer mit y der Form (n,) aufgerufen, wobei n = len(y0) ist.

Wenn vectorized True ist, kann fun mit y der Form (n, k) aufgerufen werden, wobei k eine Ganzzahl ist. In diesem Fall muss fun so funktionieren, dass fun(t, y)[:, i] == fun(t, y[:, i]) (d. h. jede Spalte des zurückgegebenen Arrays ist die Zeitableitung des Zustands, der einer Spalte von y entspricht).

Das Setzen von vectorized=True ermöglicht eine schnellere finite Differenzen-Approximation des Jacobi-Matrix für die Methoden ‘Radau’ und ‘BDF’, führt aber zu einer langsameren Ausführung für andere Methoden und für ‘Radau’ und ‘BDF’ unter bestimmten Umständen (z. B. kleine len(y0)).

argstuple, optional

Zusätzliche Argumente, die an die benutzerdefinierten Funktionen übergeben werden sollen. Wenn angegeben, werden die zusätzlichen Argumente an alle benutzerdefinierten Funktionen übergeben. Wenn also beispielsweise fun die Signatur fun(t, y, a, b, c) hat, dann müssen jac (falls angegeben) und alle Ereignisfunktionen die gleiche Signatur haben und args muss ein Tupel der Länge 3 sein.

**options

An den gewählten Löser übergebene Optionen. Alle verfügbaren Optionen für bereits implementierte Löser sind unten aufgelistet.

first_stepfloat or None, optional

Anfängliche Schrittweite. Standard ist None, was bedeutet, dass der Algorithmus dies wählen sollte.

max_stepfloat, optional

Maximale zulässige Schrittgröße. Standard ist np.inf, d.h. die Schrittgröße ist nicht begrenzt und wird ausschließlich vom Solver bestimmt.

rtol, atolFloat oder Array-ähnlich, optional

Relative und absolute Toleranzen. Der Löser hält die lokalen Fehlerabschätzungen kleiner als atol + rtol * abs(y). Hier steuert rtol die relative Genauigkeit (Anzahl korrekter Ziffern), während atol die absolute Genauigkeit (Anzahl korrekter Dezimalstellen) steuert. Um die gewünschte rtol zu erreichen, setzen Sie atol kleiner als den kleinsten Wert, der von rtol * abs(y) erwartet werden kann, sodass rtol den erlaubten Fehler dominiert. Wenn atol größer als rtol * abs(y) ist, ist die Anzahl der korrekten Ziffern nicht garantiert. Umgekehrt, um die gewünschte atol zu erreichen, setzen Sie rtol so, dass rtol * abs(y) immer kleiner als atol ist. Wenn Komponenten von y unterschiedliche Skalen haben, kann es vorteilhaft sein, unterschiedliche atol-Werte für verschiedene Komponenten festzulegen, indem Array-ähnliches mit der Form (n,) für atol übergeben wird. Standardwerte sind 1e-3 für rtol und 1e-6 für atol.

jacArray-ähnlich, dünn besetztes Matrix, aufrufbar oder None, optional

Jacobi-Matrix der rechten Seite des Systems in Bezug auf y, erforderlich für die Methoden ‘Radau’, ‘BDF’ und ‘LSODA’. Die Jacobi-Matrix hat die Form (n, n) und ihr Element (i, j) ist gleich d f_i / d y_j. Es gibt drei Möglichkeiten, die Jacobi-Matrix zu definieren:

Wenn Array-ähnlich oder dünn besetztes Matrix, wird angenommen, dass die Jacobi-Matrix konstant ist. Nicht unterstützt von ‘LSODA’.

Wenn aufrufbar, wird angenommen, dass die Jacobi-Matrix sowohl von t als auch von y abhängt; sie wird bei Bedarf als jac(t, y) aufgerufen. Zusätzliche Argumente müssen übergeben werden, wenn args verwendet wird (siehe Dokumentation des Arguments args). Für die Methoden ‘Radau’ und ‘BDF’ kann der Rückgabewert eine dünn besetzte Matrix sein.

Wenn None (Standard), wird die Jacobi-Matrix durch endliche Differenzen angenähert.

Es wird generell empfohlen, die Jacobi-Matrix bereitzustellen, anstatt sich auf eine Approximation durch endliche Differenzen zu verlassen.

jac_sparsityArray-ähnlich, dünn besetztes Matrix oder None, optional

Definiert die Sparsity-Struktur der Jacobi-Matrix für eine finite Differenzen-Approximation. Ihre Form muss (n, n) sein. Dieses Argument wird ignoriert, wenn jac nicht None ist. Wenn die Jacobi-Matrix in jeder Zeile nur wenige Nicht-Null-Elemente hat, wird die Angabe der Sparsity-Struktur die Berechnungen erheblich beschleunigen [10]. Ein Nulleintrag bedeutet, dass ein entsprechendes Element in der Jacobi-Matrix immer Null ist. Wenn None (Standard), wird angenommen, dass die Jacobi-Matrix dicht besetzt ist. Nicht unterstützt von ‘LSODA’, siehe stattdessen lband und uband.

lband, ubandInt oder None, optional

Parameter, die die Bandbreite der Jacobi-Matrix für die Methode ‘LSODA’ definieren, d. h., jac[i, j] != 0 nur für i - lband <= j <= i + uband. Standard ist None. Das Setzen dieser Werte erfordert, dass Ihre jac-Routine die Jacobi-Matrix im gepackten Format zurückgibt: das zurückgegebene Array muss n Spalten und uband + lband + 1 Zeilen haben, in denen die Diagonalen der Jacobi-Matrix geschrieben sind. Genauer gesagt jac_packed[uband + i - j , j] = jac[i, j]. Das gleiche Format wird in scipy.linalg.solve_banded verwendet (siehe Abbildung). Diese Parameter können auch mit jac=None verwendet werden, um die Anzahl der durch endliche Differenzen geschätzten Jacobi-Elemente zu reduzieren.

min_stepFloat, optional

Die minimal zulässige Schrittweite für die Methode ‘LSODA’. Standardmäßig ist min_step Null.

Rückgabe:

Bunch-Objekt mit den folgenden definierten Feldern

tndarray, Form (n_points,)

Zeitpunkte.

yndarray, Form (n, n_points)

Werte der Lösung bei t.

solOdeSolution oder None

Gefundene Lösung als OdeSolution-Instanz; None, wenn dense_output auf False gesetzt war.

t_eventsListe von ndarrays oder None

Enthält für jeden Ereignistyp eine Liste von Arrays, an denen ein Ereignis dieses Typs erkannt wurde. None, wenn events None war.

y_eventsListe von ndarrays oder None

Für jeden Wert von t_events der entsprechende Wert der Lösung. None, wenn events None war.

nfevint

Anzahl der Auswertungen der rechten Seite.

njevint

Anzahl der Auswertungen der Jacobi-Matrix.

nluint

Anzahl der LU-Zerlegungen.

statusint

Grund für die Beendigung des Algorithmus

-1: Integrationsschritt fehlgeschlagen.

0: Der Löser hat das Ende von tspan erfolgreich erreicht.

1: Ein terminierendes Ereignis ist aufgetreten.

messageString

Menschenlesbare Beschreibung des Abbruchgrundes.

successbool

True, wenn der Löser das Intervallende erreicht hat oder ein terminierendes Ereignis aufgetreten ist (status >= 0).

Referenzen

[1]

J. R. Dormand, P. J. Prince, „A family of embedded Runge-Kutta formulae“, Journal of Computational and Applied Mathematics, Vol. 6, No. 1, S. 19-26, 1980.

[2]

L. W. Shampine, „Some Practical Runge-Kutta Formulas“, Mathematics of Computation, Vol. 46, No. 173, S. 135-150, 1986.

[3]

P. Bogacki, L.F. Shampine, „A 3(2) Pair of Runge-Kutta Formulas“, Appl. Math. Lett. Vol. 2, No. 4. S. 321-325, 1989.

[4]

E. Hairer, G. Wanner, „Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems“, Kap. IV.8.

[5]

Backward Differentiation Formula auf Wikipedia.

[6]

L. F. Shampine, M. W. Reichelt, „THE MATLAB ODE SUITE“, SIAM J. SCI. COMPUTE., Vol. 18, No. 1, S. 1-22, Januar 1997.

[7]

A. C. Hindmarsh, „ODEPACK, A Systematized Collection of ODE Solvers“, IMACS Transactions on Scientific Computation, Vol 1., S. 55-64, 1983.

[8]

L. Petzold, „Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations“, SIAM Journal on Scientific and Statistical Computing, Vol. 4, No. 1, S. 136-148, 1983.

[9]

Steife Gleichung auf Wikipedia.

[10]

A. Curtis, M. J. D. Powell und J. Reid, „On the estimation of sparse Jacobian matrices“, Journal of the Institute of Mathematics and its Applications, 13, S. 117-120, 1974.

[11]

Cauchy-Riemann-Gleichungen auf Wikipedia.

[12]

Lotka-Volterra-Gleichungen auf Wikipedia.

[13]

E. Hairer, S. P. Norsett G. Wanner, „Solving Ordinary Differential Equations I: Nonstiff Problems“, Kap. II.

[14]

Seite mit dem ursprünglichen Fortran-Code von DOP853.

Beispiele

Einfaches exponentielles Abklingen, das automatisch gewählte Zeitpunkte zeigt.

>>> import numpy as np
>>> from scipy.integrate import solve_ivp
>>> def exponential_decay(t, y): return -0.5 * y
>>> sol = solve_ivp(exponential_decay, [0, 10], [2, 4, 8])
>>> print(sol.t)
[ 0.          0.11487653  1.26364188  3.06061781  4.81611105  6.57445806
  8.33328988 10.        ]
>>> print(sol.y)
[[2.         1.88836035 1.06327177 0.43319312 0.18017253 0.07483045
  0.03107158 0.01350781]
 [4.         3.7767207  2.12654355 0.86638624 0.36034507 0.14966091
  0.06214316 0.02701561]
 [8.         7.5534414  4.25308709 1.73277247 0.72069014 0.29932181
  0.12428631 0.05403123]]

Spezifikation von Zeitpunkten, an denen die Lösung gewünscht wird.

>>> sol = solve_ivp(exponential_decay, [0, 10], [2, 4, 8],
...                 t_eval=[0, 1, 2, 4, 10])
>>> print(sol.t)
[ 0  1  2  4 10]
>>> print(sol.y)
[[2.         1.21305369 0.73534021 0.27066736 0.01350938]
 [4.         2.42610739 1.47068043 0.54133472 0.02701876]
 [8.         4.85221478 2.94136085 1.08266944 0.05403753]]

Eine Kanonenkugel wird nach oben geschossen und trifft mit einem terminierenden Ereignis auf den Boden. Die Felder terminal und direction eines Ereignisses werden durch Monkey-Patching einer Funktion angewendet. Hier ist y[0] die Position und y[1] die Geschwindigkeit. Das Projektil startet bei Position 0 mit Geschwindigkeit +10. Beachten Sie, dass die Integration niemals t=100 erreicht, da das Ereignis terminierend ist.

>>> def upward_cannon(t, y): return [y[1], -0.5]
>>> def hit_ground(t, y): return y[0]
>>> hit_ground.terminal = True
>>> hit_ground.direction = -1
>>> sol = solve_ivp(upward_cannon, [0, 100], [0, 10], events=hit_ground)
>>> print(sol.t_events)
[array([40.])]
>>> print(sol.t)
[0.00000000e+00 9.99900010e-05 1.09989001e-03 1.10988901e-02
 1.11088891e-01 1.11098890e+00 1.11099890e+01 4.00000000e+01]

Verwendung von dense_output und events, um die Position 100 am Scheitelpunkt der Flugbahn der Kanonenkugel zu finden. Der Scheitelpunkt ist nicht als terminierend definiert, daher werden sowohl der Scheitelpunkt als auch der Bodenkontakt gefunden. Bei t=20 liegen keine Informationen vor, daher wird das Attribut sol zur Auswertung der Lösung verwendet. Das Attribut sol wird zurückgegeben, indem dense_output=True gesetzt wird. Alternativ kann das Attribut y_events verwendet werden, um auf die Lösung zum Zeitpunkt des Ereignisses zuzugreifen.

>>> def apex(t, y): return y[1]
>>> sol = solve_ivp(upward_cannon, [0, 100], [0, 10],
...                 events=(hit_ground, apex), dense_output=True)
>>> print(sol.t_events)
[array([40.]), array([20.])]
>>> print(sol.t)
[0.00000000e+00 9.99900010e-05 1.09989001e-03 1.10988901e-02
 1.11088891e-01 1.11098890e+00 1.11099890e+01 4.00000000e+01]
>>> print(sol.sol(sol.t_events[1][0]))
[100.   0.]
>>> print(sol.y_events)
[array([[-5.68434189e-14, -1.00000000e+01]]),
 array([[1.00000000e+02, 1.77635684e-15]])]

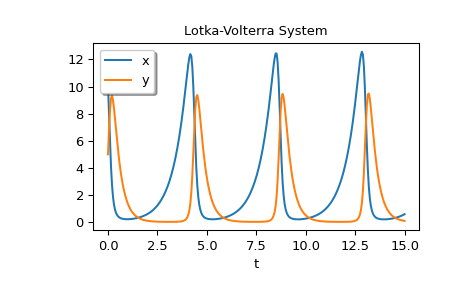
Als Beispiel für ein System mit zusätzlichen Parametern implementieren wir die Lotka-Volterra-Gleichungen [12].

>>> def lotkavolterra(t, z, a, b, c, d):
...     x, y = z
...     return [a*x - b*x*y, -c*y + d*x*y]
...

Wir übergeben die Parameterwerte a=1.5, b=1, c=3 und d=1 mit dem Argument args.

>>> sol = solve_ivp(lotkavolterra, [0, 15], [10, 5], args=(1.5, 1, 3, 1),
...                 dense_output=True)

Berechnung einer dichten Lösung und deren Plotten.

>>> t = np.linspace(0, 15, 300)
>>> z = sol.sol(t)
>>> import matplotlib.pyplot as plt
>>> plt.plot(t, z.T)
>>> plt.xlabel('t')
>>> plt.legend(['x', 'y'], shadow=True)
>>> plt.title('Lotka-Volterra System')
>>> plt.show()

../../_images/scipy-integrate-solve_ivp-1_00_00.png

Ein paar Beispiele für die Verwendung von solve_ivp zur Lösung der Differentialgleichung y' = Ay mit einer komplexen Matrix A.

>>> A = np.array([[-0.25 + 0.14j, 0, 0.33 + 0.44j],
...               [0.25 + 0.58j, -0.2 + 0.14j, 0],
...               [0, 0.2 + 0.4j, -0.1 + 0.97j]])

Lösen eines IVP mit A aus dem obigen Beispiel und y als 3x1-Vektor.

>>> def deriv_vec(t, y):
...     return A @ y
>>> result = solve_ivp(deriv_vec, [0, 25],
...                    np.array([10 + 0j, 20 + 0j, 30 + 0j]),
...                    t_eval=np.linspace(0, 25, 101))
>>> print(result.y[:, 0])
[10.+0.j 20.+0.j 30.+0.j]
>>> print(result.y[:, -1])
[18.46291039+45.25653651j 10.01569306+36.23293216j
 -4.98662741+80.07360388j]

Lösen eines IVP mit A aus dem obigen Beispiel mit y als 3x3-Matrix.

>>> def deriv_mat(t, y):
...     return (A @ y.reshape(3, 3)).flatten()
>>> y0 = np.array([[2 + 0j, 3 + 0j, 4 + 0j],
...                [5 + 0j, 6 + 0j, 7 + 0j],
...                [9 + 0j, 34 + 0j, 78 + 0j]])

>>> result = solve_ivp(deriv_mat, [0, 25], y0.flatten(),
...                    t_eval=np.linspace(0, 25, 101))
>>> print(result.y[:, 0].reshape(3, 3))
[[ 2.+0.j  3.+0.j  4.+0.j]
 [ 5.+0.j  6.+0.j  7.+0.j]
 [ 9.+0.j 34.+0.j 78.+0.j]]
>>> print(result.y[:, -1].reshape(3, 3))
[[  5.67451179 +12.07938445j  17.2888073  +31.03278837j
    37.83405768 +63.25138759j]
 [  3.39949503 +11.82123994j  21.32530996 +44.88668871j
    53.17531184+103.80400411j]
 [ -2.26105874 +22.19277664j -15.1255713  +70.19616341j
   -38.34616845+153.29039931j]]