scipy.interpolate.

CloughTocher2DInterpolator#

class scipy.interpolate.CloughTocher2DInterpolator(points, values, fill_value=nan, tol=1e-06, maxiter=400, rescale=False)#

Stückweise kubischer, C1-glatter, Krümmungsminimierender Interpolator in N=2 Dimensionen.

Hinzugefügt in Version 0.9.

Parameter:

pointsndarray von floats, Form (npoints, ndims); oder Delaunay: 2-D Array von Koordinaten der Datenpunkte oder eine vortberechnete Delaunay-Triangulierung.
valuesndarray von float oder complex, Form (npoints, …): N-D Array von Datenwerten an den points. Die Länge von values entlang der ersten Achse muss gleich der Länge von points sein. Im Gegensatz zu einigen Interpolatoren kann die Interpolationsachse nicht geändert werden.
fill_valuefloat, optional: Wert, der verwendet wird, um angeforderte Punkte außerhalb der konvexen Hülle der Eingabepunkte aufzufüllen. Wenn nicht angegeben, ist der Standardwert nan.
tolfloat, optional: Absolute/relative Toleranz für die Gradientenschätzung.
maxiterint, optional: Maximale Anzahl von Iterationen bei der Gradientenschätzung.
rescalebool, optional: Skaliert die Punkte auf einen Einheitswürfel, bevor die Interpolation durchgeführt wird. Dies ist nützlich, wenn einige der Eingabedimensionen inkommensurable Einheiten haben und sich um viele Größenordnungen unterscheiden.

Methoden

__call__(xi)

Interpolationsfunktion an gegebenen Punkten auswerten.

Siehe auch

griddata: Interpoliert unstrukturierte D-D-Daten.
LinearNDInterpolator: Stückweise lineare Interpolation in N > 1 Dimensionen.
NearestNDInterpolator: Nächstliegender Nachbar-Interpolator in N > 1 Dimensionen.
interpn: Interpolation auf einem regulären Gitter oder einem rechtwinkligen Gitter.
RegularGridInterpolator: Interpolator auf einem regulären oder rechtwinkligen Gitter in beliebigen Dimensionen (interpn umschließt diese Klasse).

Hinweise

Der Interpolant wird konstruiert, indem die Eingabedaten mit Qhull [1] trianguliert werden und auf jedem Dreieck ein stückweise kubisches interpolierendes Bezier-Polynom nach einem Clough-Tocher-Schema [CT] konstruiert wird. Der Interpolant ist garantiert stetig differenzierbar.

Die Gradienten des Interpolanten werden so gewählt, dass die Krümmung der interpolierenden Oberfläche approximativ minimiert wird. Die dafür notwendigen Gradienten werden mit dem globalen Algorithmus geschätzt, der in [Nielson83] und [Renka84] beschrieben ist.

Hinweis

Für Daten auf einem regulären Gitter verwenden Sie stattdessen interpn.

Referenzen

[1]

http://www.qhull.org/

[CT]

Siehe z. B. P. Alfeld, „A trivariate Clough-Tocher scheme for tetrahedral data“. Computer Aided Geometric Design, 1, 169 (1984); G. Farin, „Triangular Bernstein-Bezier patches“. Computer Aided Geometric Design, 3, 83 (1986).

[Nielson83]

G. Nielson, „A method for interpolating scattered data based upon a minimum norm network“. Math. Comp., 40, 253 (1983).

[Renka84]

R. J. Renka und A. K. Cline. „A Triangle-based C1 interpolation method.“, Rocky Mountain J. Math., 14, 223 (1984).

Beispiele

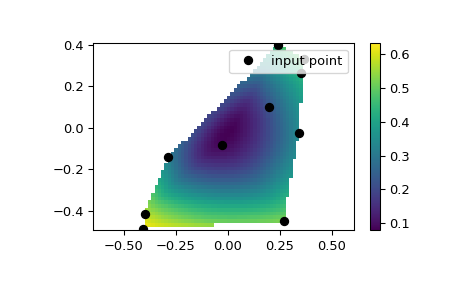
Wir können Werte auf einer 2D-Ebene interpolieren

>>> from scipy.interpolate import CloughTocher2DInterpolator
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> x = rng.random(10) - 0.5
>>> y = rng.random(10) - 0.5
>>> z = np.hypot(x, y)
>>> X = np.linspace(min(x), max(x))
>>> Y = np.linspace(min(y), max(y))
>>> X, Y = np.meshgrid(X, Y)  # 2D grid for interpolation
>>> interp = CloughTocher2DInterpolator(list(zip(x, y)), z)
>>> Z = interp(X, Y)
>>> plt.pcolormesh(X, Y, Z, shading='auto')
>>> plt.plot(x, y, "ok", label="input point")
>>> plt.legend(loc="upper right")
>>> plt.colorbar()
>>> plt.axis("equal")
>>> plt.show()

../../_images/scipy-interpolate-CloughTocher2DInterpolator-1.png